题目内容
在一个盒子中,放有标号分别为1,2,3的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为x、y,设O为坐标原点,设M的坐标为(x-2,x-y).
(1)求|
|2的所有取值之和;
(2)求事件“|
|2取得最大值”的概率.
(1)求|
| OM |
(2)求事件“|
| OM |
考点:几何概型,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由题意,x,y可能的取值为1,2,3,列举出所有(x-2,x-y)的所有可能取值以及|
|2的取值;
(2)由(1)可知,由于|
|2取最大值5时,x,y的取值为(1,3),(3,1)共2种,由概率公式可求.
| OM |
(2)由(1)可知,由于|
| OM |
解答:
解:(1)由题意,x,y可能的取值为1,2,3,….(1分)
则(x-2,x-y)的所有可能取值为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共有9种 ….(4分)
由|
|2的=(x-2)2+(x-y)2可知|
|2的所有可能值为0,1,2,5
故|
|2的所有可能取值之和为8 ….(8分)
(2)由于|
|2取最大值5时,x,y的取值为(1,3),(3,1)共2种 ….(10分)
故求事件“|
|2取得最大值”的概率为
…(12分)
则(x-2,x-y)的所有可能取值为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共有9种 ….(4分)
由|
| OM |
| OM |
故|
| OM |
(2)由于|
| OM |
故求事件“|
| OM |
| 2 |
| 9 |
点评:本题考查了古典概型概率的求法;关键是利用列举的方法求出满足条件的事件,再由公式求值.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
某小学教师准备购买一些签字笔和铅笔盒作为奖品,已知签字笔每支5元,铅笔盒每个6元,花费总额不能超过50元.为了便于学生选择,购买签字笔和铅笔盒的个数均不能少于3个,那么该教师有 种不同的购买奖品方案.
设2x=5y=m,且
+
=2,则m的值是( )
| 1 |
| x |
| 1 |
| y |
A、±
| ||
B、
| ||
| C、10 | ||
| D、100 |
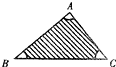 △ABC中,AB=8,AC=6,BC=10,顶点A、B、C处分别有一枚半径为1的硬币(顶点A、B、C分别与硬币的中心重合).向△ABC内部投一点,那么该点落在阴影部分的概率为( )
△ABC中,AB=8,AC=6,BC=10,顶点A、B、C处分别有一枚半径为1的硬币(顶点A、B、C分别与硬币的中心重合).向△ABC内部投一点,那么该点落在阴影部分的概率为( )A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
函数y=(sinx-cosx)2的最小正周期为( )
| A、2π | ||
B、
| ||
| C、π | ||
D、
|
已知平面向量
=(2,1),
=(-4,k),且
⊥
,则3
+2
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(-2,4) |
| B、( 4,7) |
| C、(-2,19) |
| D、(19,2) |
已知全集U=R,集合A={x|x+1>0},B={x|y=loga(x+2)},则集合(∁UA)∩B=( )
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-∞,-2) |
| D、(-1,-∞) |
 已知函数
已知函数