题目内容
 已知函数f(x)=2sin(
已知函数f(x)=2sin(| 2π |
| 3 |
| π |
| 6 |
(Ⅰ)请用“五点法”画出函数f(x)在一个周期上的图象(先列表,再画图);
(Ⅱ)求f(x)的单调增区间;
(Ⅲ)求f(x)在[-
| 1 |
| 2 |
| 3 |
| 4 |
考点:五点法作函数y=Asin(ωx+φ)的图象,正弦函数的单调性,三角函数的最值
专题:图表型,三角函数的图像与性质
分析:(Ⅰ)先列表,再描点画图即可用“五点法”画出函数f(x)在一个周期上的图象;
(Ⅱ)由2kπ-
≤
x+
≤2kπ+
(k∈Z),可解得f(x)的单调增区间;
(Ⅲ)由x∈[-
,
],可得
x+
∈[-
,
],从而求得f(x)在[-
,
]上的取值范围.
(Ⅱ)由2kπ-
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
(Ⅲ)由x∈[-
| 1 |
| 2 |
| 3 |
| 4 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
解答:
本题满分(13分)
解:(Ⅰ)函数f(x)=2sin(
x+
)的周期T=3,-----------------------------------(1分)
列表如下:
描点画图如图所示.--------------------------------------------------(5分)
(Ⅱ)函数y=sinx的单调增区间为[2kπ-
,2kπ+
](k∈Z).-----------------------(6分)
由2kπ-
≤
x+
≤2kπ+
(k∈Z),
得3k-1≤x≤3k+
(k∈Z).
所以f(x)单调增区间为[3k-1,3k+
](k∈Z).----------------------------------------------(9分)
(Ⅲ)因为x∈[-
,
],
所以
x+
∈[-
,
],
所以sin(
x+
)∈[-
,1]
所以2sin(
x+
)∈[-1,2],即f(x)在[-
,
]上的取值范围是[-1,2].-------------(13分)
说明:(Ⅱ)(Ⅲ)问,如果最终结果错误,可细化解题步骤给过程分;如果仅有最终正确结果,无步骤每问各扣(1分).
解:(Ⅰ)函数f(x)=2sin(
| 2π |
| 3 |
| π |
| 6 |

列表如下:
| 0 |
| π |
| 2π | ||||||||
| x | -
|
|
| 2 |
| ||||||||
| f(x) | 0 | 2 | 0 | -2 | 0 |
(Ⅱ)函数y=sinx的单调增区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
由2kπ-
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
得3k-1≤x≤3k+
| 1 |
| 2 |
所以f(x)单调增区间为[3k-1,3k+
| 1 |
| 2 |
(Ⅲ)因为x∈[-
| 1 |
| 2 |
| 3 |
| 4 |
所以
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
所以sin(
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
所以2sin(
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 4 |
说明:(Ⅱ)(Ⅲ)问,如果最终结果错误,可细化解题步骤给过程分;如果仅有最终正确结果,无步骤每问各扣(1分).
点评:本题主要考察了五点法作函数y=Asin(ωx+φ)的图象,正弦函数的单调性,三角函数的最值的解法,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) 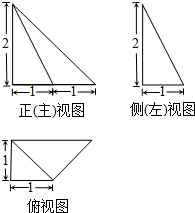

A、最长棱的棱长为
| ||
| B、最长棱的棱长为3 | ||
| C、侧面四个三角形中有且仅有一个是正三角形 | ||
| D、侧面四个三角形都是直角三角形 |
在区间[0,1]上任取2个数a,b,若向量
=(a,b),则|
|≤1的概率是( )
| m |
| m |
A、
| ||
B、
| ||
C、
| ||
D、
|