题目内容
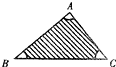△ABC中，AB=8，AC=6，BC=10，顶点A、B、C处分别有一枚半径为1的硬币（顶点A、B、C分别与硬币的中心重合）．向△ABC内部投一点，那么该点落在阴影部分的概率为（ ）A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：由题意，概率符合几何概型，所以只要求出阴影部分的面积，根据三角形的内角和得到空白部分的面积是以1为半径的半圆的面积，由几何概型的概率公式可求．
解答：
解：由题意，题目符合几何概型，
△ABC中，AB=8，AC=6，BC=10，所以三角形为直角三角形，面积为
×AB×AC=24，
阴影部分的面积为：三角形面积-
圆面积=24-
，
所以点落在阴影部分的概率为
=1-
；
故选B
△ABC中，AB=8，AC=6，BC=10，所以三角形为直角三角形，面积为| 1 |
| 2 |
阴影部分的面积为：三角形面积-
| 1 |
| 2 |
| π |
| 2 |
所以点落在阴影部分的概率为
24-
| ||
| 24 |
| π |
| 48 |
故选B
点评：本题考查了几何概型的概率求法；关键明确概率模型，然后求出满足条件的事件的集合，由概率公式解答．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
设D为不等式组
表示的平面区域，点B（a，b）为坐标平面xOy内一点，若对于区域D内的任一点A（x，y），都有
•
≤1成立，则a+b的最大值等于（ ）
|
| OA |
| OB |
| A、2 | B、1 | C、0 | D、3 |
在区间[0，1]上任取2个数a，b，若向量
=（a，b），则|
|≤1的概率是（ ）
| m |
| m |
A、
| ||
B、
| ||
C、
| ||
D、
|
平面向量
，
满足
=2
如果
=（1，1），那么
等于（ ）
| a |
| b |
| b |
| a |
| a |
| b |
| A、-（2，2） |
| B、（-2，-2） |
| C、（2，-2） |
| D、（2，2） |