题目内容
19.命题“?m∈[0,1],x+$\frac{1}{x}$≥2”的否定形式是( )| A. | ?m∈[0,1],x+$\frac{1}{x}$<2 | B. | ?m∈[0,1],x+$\frac{1}{x}$≥2 | ||
| C. | ?m∈(-∞,0)∪(0,+∞),x+$\frac{1}{x}$≥2 | D. | ?m∈[0,1],x+$\frac{1}{x}$<2 |
分析 利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题“?m∈[0,1],x+$\frac{1}{x}$≥2”的否定形式是:?m∈[0,1],x+$\frac{1}{x}$<2.
故选:D.
点评 本题考查特称命题与全称命题的否定关系,是基础题.

练习册系列答案
相关题目
9.下列关于命题的说法错误的是( )
| A. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| B. | 命题“若随机变量X~N(1,4),P(X≤0)=m,则P(0<X<2)=1-2m”为真命题 | |
| C. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| D. | 若命题P:?n∈N,2n>1000,则?P:?n∈N,2n>1000 |
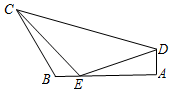 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.