题目内容
14.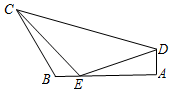 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.则CD=7.
分析 在△CBE中,由余弦定理得CE2=BE2+CB2-2BE•CBcos120°,得CB.由余弦定理得CB2=BE2+CE2-2BE•CEcos∠BEC⇒cos∠BEC⇒sin∠BEC、cos∠AED在直角△ADE中,求得DE=2$\sqrt{7}$,在△CED中,由余弦定理得CD2=CE2+DE2-2CE•DEcos120°即可
解答 解:在△CBE中,由余弦定理得CE2=BE2+CB2-2BE•CBcos120°,
即7=1+CB2+CB,解得CB=2.
由余弦定理得CB2=BE2+CE2-2BE•CEcos∠BEC⇒cos∠BEC=$\frac{2\sqrt{7}}{7}$,
⇒sin∠BEC=$\frac{\sqrt{21}}{7}$.
sin∠AED=sin(1200+∠BEC)=$\frac{\sqrt{3}}{2}×\frac{2\sqrt{7}}{7}-\frac{1}{2}×\frac{\sqrt{21}}{7}=\frac{\sqrt{21}}{14}$,
⇒cos∠AED=$\frac{5\sqrt{7}}{14}$.
在直角△ADE中,AE=5,cos$∠AED=\frac{AE}{DE}=\frac{5\sqrt{7}}{14}$,⇒DE=2$\sqrt{7}$,
在△CED中,由余弦定理得CD2=CE2+DE2-2CE•DEcos120°=49
∴CD=7.
故答案为:7
点评 本题考查了正余弦定理在解三角形中的应用,是中档题

练习册系列答案
相关题目
4.已知复数$z=\frac{5i}{3-4i}$(i是虚数单位),则|z|=( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
5.已知集合M={0,1},集合N满足M∪N={0,1},则集合N共有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.命题“?m∈[0,1],x+$\frac{1}{x}$≥2”的否定形式是( )
| A. | ?m∈[0,1],x+$\frac{1}{x}$<2 | B. | ?m∈[0,1],x+$\frac{1}{x}$≥2 | ||
| C. | ?m∈(-∞,0)∪(0,+∞),x+$\frac{1}{x}$≥2 | D. | ?m∈[0,1],x+$\frac{1}{x}$<2 |
6.定积分${∫}_{1}^{e}$$\frac{1}{x}$dx的值等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.
已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.