题目内容
7.若函数f(x)=$\left\{\begin{array}{l}{x+{2}^{x},x≤0}\\{\frac{x}{a}-lnx,x>0}\end{array}\right.$,在其定义域上恰有两个零点,则正实数a的值为e.分析 根据函数图象可知f(x)在(-∞,0]上有1个零点,故f(x)在(0,+∞)上有1个零点,根据导数的几何意义求出a即可.
解答 解:当x≤0时,令f(x)=0得2x=-x,
作出y=2x与y=-x的函数图形如图所示: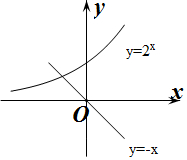
由图象可知f(x)在(-∞,0]上有唯一一个零点.
∵f(x)有两个零点,
∴f(x)在(0,+∞)上有唯一一个零点.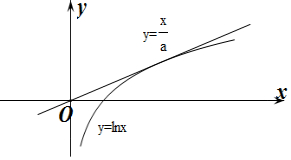
∴直线y=$\frac{x}{a}$与曲线y=lnx相切,设切点坐标为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=\frac{{x}_{0}}{a}}\\{{y}_{0}=ln{x}_{0}}\\{\frac{1}{{x}_{0}}=\frac{1}{a}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{0}=e}\\{{y}_{0}=1}\\{a=e}\end{array}\right.$.
故答案为:e.
点评 本题考查了函数零点与函数图象的关系,导数的几何意义,属于中档题.

练习册系列答案
相关题目
17.在区间[0,4]上随机取两个数x,y,则xy∈[0,4]的概率是( )
| A. | $\frac{2-ln4}{4}$ | B. | $\frac{3-2ln4}{4}$ | C. | $\frac{1+ln4}{4}$ | D. | $\frac{1+2ln4}{4}$ |
18.已知定义域为R的奇函数f(x)满足f(3-x)+f(x)=0,且当$x∈({-\frac{3}{2},0})$时,f(x)=log2(2x+7),则f(2017)=( )
| A. | -2 | B. | log23 | C. | 3 | D. | -log25 |
19.命题“?m∈[0,1],x+$\frac{1}{x}$≥2”的否定形式是( )
| A. | ?m∈[0,1],x+$\frac{1}{x}$<2 | B. | ?m∈[0,1],x+$\frac{1}{x}$≥2 | ||
| C. | ?m∈(-∞,0)∪(0,+∞),x+$\frac{1}{x}$≥2 | D. | ?m∈[0,1],x+$\frac{1}{x}$<2 |
16.已知F是椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左焦点,设动点P在椭圆上,若直线FP的斜率大于$\sqrt{3}$,则直线OP(O为原点)的斜率的取值范围是( )
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{2}}]∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}}]$ | C. | $({-∞,-\frac{3}{2}})∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}})$ | D. | $[{-\frac{3}{2},+∞})$ |