题目内容
（1）求值：sin50°（1+
tan10°）；
（2）已知sin（α+2β）=3sinα，求
的值．
| 3 |
（2）已知sin（α+2β）=3sinα，求
| tan(α+β) |
| tanβ |
考点：三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：（1）首先，将正切化成正弦和余弦的表示形式，然后，借助于辅助角公式进行化简，最后结合二倍角公式进行化简即可；
（2）首先，给定的角进行变形：α+2β=（α+β）+β，α=（α+β）-β，然后，借助于两角和与差的三角函数进行化简，从而得到结果．
（2）首先，给定的角进行变形：α+2β=（α+β）+β，α=（α+β）-β，然后，借助于两角和与差的三角函数进行化简，从而得到结果．
解答：
（1）解：原式=sin50°（1+
）
=sin50°
=sin50°
=
=
=1，
（2）解：∵α+2β=（α+β）+β，α=（α+β）-β，
∴sin（α+2β）=sin[（α+β）+β]，3sinα=3sin[（α+β）-β]，
∴sin[（α+β）+β]=3sin[（α+β）-β]，
∴sin（α+β）cosβ+cos（α+β）sinβ=3sin（α+β）cosβ-3cos（α+β）sinβ，
∴sin（α+β）cosβ=2cos（α+β）sinβ，
∴
=2，
∴
的值2．
| 3 |
| sin10° |
| cos10° |
=sin50°
cos10°+
| ||
| cos10° |
=sin50°
| 2sin(30°+10°) |
| cos10° |
=
| 2sin40°cos40° |
| cos10° |
=
| sin80° |
| cos10° |
=1，
（2）解：∵α+2β=（α+β）+β，α=（α+β）-β，
∴sin（α+2β）=sin[（α+β）+β]，3sinα=3sin[（α+β）-β]，
∴sin[（α+β）+β]=3sin[（α+β）-β]，
∴sin（α+β）cosβ+cos（α+β）sinβ=3sin（α+β）cosβ-3cos（α+β）sinβ，
∴sin（α+β）cosβ=2cos（α+β）sinβ，
∴
| tan(α+β) |
| tanβ |
∴
| tan(α+β) |
| tanβ |
点评：本两题重点考查了三角恒等变换公式及其灵活运用，注意角的灵活拆分等知识，属于中档题．
练习册系列答案
相关题目
不等式（
） x2+ax＜（
）2x+a-2恒成立，则a的取值范围是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、[-2，2] |
| B、（-2，2） |
| C、[0，2] |
| D、[-3，3] |
“x＞3”是“x2＞9”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既充分又必要条件 |
| D、既不充分又不必要条件 |
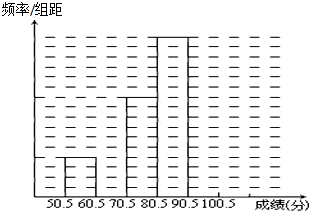某中学举行了一次“环保知识竞赛”，共有800名学生参加了这次竞赛．从中抽取了部分学生的成绩进行统计．请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：