题目内容
已知曲线C上任意一点P到点F（0，1）的距离比它到直线l：y=-2的距离小1，一个圆的圆心为A（0，4），过点A的直线与曲线C交于D，E两点．
（Ⅰ）求曲线C的方程；
（Ⅱ）当线段DE长度最短时，曲线C过D点的切线与圆A相切的弦长为
，求此时圆A的方程．
（Ⅰ）求曲线C的方程；
（Ⅱ）当线段DE长度最短时，曲线C过D点的切线与圆A相切的弦长为
8
| ||
| 5 |
考点：圆与圆锥曲线的综合
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）根据抛物线的定义，即可求曲线C的方程；
（Ⅱ）根据直线和圆的位置关系，以及相应的弦长公式，求出圆的圆心和半径，即可求出圆的方程．
（Ⅱ）根据直线和圆的位置关系，以及相应的弦长公式，求出圆的圆心和半径，即可求出圆的方程．
解答：
解：（Ⅰ）点P到点F（0，1）的距离比它到直线l：y=-2的距离小1，
即P在直线l的上方，且P到点F（0，1）的距离与它到直线l：y=-1的距离相等，
即P点的轨迹是以F为焦点，l为准线的抛物线，则对应的抛物线方程为x2=4y．
（Ⅱ）设直线DE：y=kx+4，
由
，得x2-4kx-16=0，
则x1+x2=4k，x1x2=-16，
则DE=
=4
，
则当k=0时，DE最短，不妨设D在第一象限，此时D（4，4），
过D的切线为2x-y-4=0，
过D点的切线与圆A相切的弦长2
=
，
解得R=4，
则圆的方程为x2+（y-4）2=16．
即P在直线l的上方，且P到点F（0，1）的距离与它到直线l：y=-1的距离相等，
即P点的轨迹是以F为焦点，l为准线的抛物线，则对应的抛物线方程为x2=4y．
（Ⅱ）设直线DE：y=kx+4，
由
|
则x1+x2=4k，x1x2=-16，
则DE=
| (1+k2)(16k2+64) |
| k4+5k2+4 |
则当k=0时，DE最短，不妨设D在第一象限，此时D（4，4），
过D的切线为2x-y-4=0，
过D点的切线与圆A相切的弦长2
R2-(
|
8
| ||
| 5 |
解得R=4，
则圆的方程为x2+（y-4）2=16．
点评：本题主要考查抛物线的定义和方程的应用，利用直线和圆的位置关系的应用，综合性较强，难度较大．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、钝角不一定是第二象限的角 |
| B、终边相同的角一定相等 |
| C、终边与始边重合的角是零角 |
| D、相等的角终边相同 |
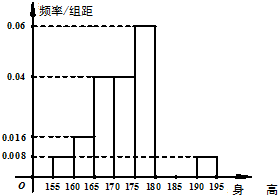从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．