题目内容
若定义域在[0,1]的函数f(x)满足:
①对于任意x1,x2∈[0,1],当x1<x2时,都有f(x1)≥f(x2);
②f(0)=0;
③f(
)=
f(x);
④f(1-x)+f(x)=-1,
则f(
)+f(
)=( )
①对于任意x1,x2∈[0,1],当x1<x2时,都有f(x1)≥f(x2);
②f(0)=0;
③f(
| x |
| 3 |
| 1 |
| 2 |
④f(1-x)+f(x)=-1,
则f(
| 1 |
| 3 |
| 9 |
| 2014 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
考点:函数的值
专题:计算题,函数的性质及应用
分析:由题意给出的四个性质可推出在[
,
]上,f(x)≡-
;从而求出f(
)+f(
)的值.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 9 |
| 2014 |
解答:
解:∵f(1-x)+f(x)=-1,令x=0;
∴f(1)+f(0)=-1,又∵f(0)=0;
∴f(1)=-1;
令x=
可得,2f(
)=-1,∴f(
)=-
;
在f(
)=
f(x)中令x=1,
则f(
)=
f(1)=-
,
又∵对于任意x1,x2∈[0,1],当x1<x2时,都有f(x1)≥f(x2);
∴在[
,
]上,f(x)≡-
.
f(
)=
•f(
)=(
)2f(
)
=(
)3•f(
)=(
)4•f(
),
=-
.
故f(
)+f(
)=-
-
=-
;
故选B.
∴f(1)+f(0)=-1,又∵f(0)=0;
∴f(1)=-1;
令x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在f(
| x |
| 3 |
| 1 |
| 2 |
则f(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵对于任意x1,x2∈[0,1],当x1<x2时,都有f(x1)≥f(x2);
∴在[
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
f(
| 9 |
| 2014 |
| 1 |
| 2 |
| 27 |
| 2014 |
| 1 |
| 2 |
| 81 |
| 2014 |
=(
| 1 |
| 2 |
| 243 |
| 2014 |
| 1 |
| 2 |
| 729 |
| 2014 |
=-
| 1 |
| 32 |
故f(
| 1 |
| 3 |
| 9 |
| 2014 |
| 1 |
| 2 |
| 1 |
| 32 |
| 17 |
| 32 |
故选B.
点评:本题考查了学生对新知识的接受与应用能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1:3,这截面把圆锥母线分成的两段的比是( )
| A、1:3 | ||
B、1:(
| ||
| C、1:9 | ||
D、
|
三个人独立地破译一个密码,他们能单独译出的概率分别为
,
,
,假设他们破译密码是彼此独立的,则此密码被破译出的概率为( )
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
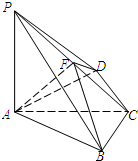 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.