题目内容
已知f(x)=-(
)x+m(
)x+3(-1≤x≤1)的最大值为4,求m的值.
| 1 |
| 4 |
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:分类讨论,函数的性质及应用
分析:先用换元法,令t=(
)x,将f(x)转化成关于t的一个二次函数,再配方,对m进行分类讨论,属于区间定对称轴定的情形.
| 1 |
| 2 |
解答:
解:令t=(
)x,∵-1≤x≤1,∴t∈[
,2],
f(x)=y=-t2+mt+3,对称轴为t=
,
当
≤
即m≤1时,y在[
,2]上单调递减,当t=
时,有最大值-
+
+3=4,解得m=
(舍去),
当
≥2即m≥4时,y在[
,2]上单调递增,当t=2时,有最大值-4+2m+3=4,解得m=
(舍去),
当
<
<2即1<m<4,y在[
,
]上单调递增,在[
,2]上单调递减,当t=
时,有最大值
+3=4,解得m=2或m=-2(舍去),
综上得m=2.
| 1 |
| 2 |
| 1 |
| 2 |
f(x)=y=-t2+mt+3,对称轴为t=
| m |
| 2 |
当
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| m |
| 2 |
| 5 |
| 2 |
当
| m |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
当
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| m |
| 2 |
| m |
| 2 |
| m2 |
| 4 |
综上得m=2.
点评:本题考查了:换元思想、配方去,分类讨论思想,等价转化思想,属于中档题.

练习册系列答案
相关题目
已知长方体的对角线长为4,过同一顶点的两条棱与此对角线成角均为60°,则长方体的体积是( )
A、16
| ||
B、8
| ||
C、8
| ||
D、4
|
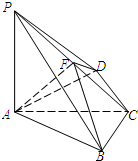 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.