题目内容
8.下列命题中错误的个数为:( )①y=$\frac{1}{2}+\frac{1}{{{2^x}-1}}$的图象关于(0,0)对称;
②y=x3+x+1的图象关于(0,1)对称;
③y=$\frac{1}{{{x^2}-1}}$的图象关于直线x=0对称;
④y=sinx+cosx的图象关于直线x=$\frac{π}{4}$对称.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据函数的奇偶性判断,①③,根据对称的定义判断②,根据三角函数的图象判断④
解答 解:①y=$\frac{1}{2}+\frac{1}{{{2^x}-1}}$,f(-x)=$\frac{1}{2}$+$\frac{1}{{2}^{-x}-1}$=$\frac{1}{2}$+$\frac{{2}^{x}}{1-{2}^{x}}$=$\frac{1}{2}$-$\frac{{2}^{x}-1+1}{{2}^{x}-1}$=-$\frac{1}{2}$-$\frac{1}{{2}^{x}-1}$=-($\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$)=-f(x),
∴函数为奇函数,则图象关于(0,0)对称,故正确
②y=x3+x+1的图象关于(0,1)对称;
由题意设对称中心的坐标为(a,b),
则有2b=f(a+x)+f(a-x)对任意x均成立,代入函数解析式得,
2b=(a+x)3+3(a+x)+1+(a-x)3+3(a-x)+1对任意x均成立,
∴a=0,b=1
即对称中心(0,1),故正确
③y=$\frac{1}{{{x^2}-1}}$的图象关于直线x=0对称,因为函数为偶函数,故函数关于y轴(x=0)对称,故正确,
④y=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)的图象关于直线x+$\frac{π}{4}$=$\frac{π}{2}$对称,即x=$\frac{π}{4}$对称,故正确.
故选:A
点评 本题考查了函数对称中心和对称轴的问题,关键是掌握其概念,属于中档题.

练习册系列答案
相关题目
16.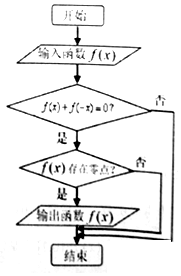 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x4 | C. | f(x)=2x | D. | f(x)=x-$\frac{1}{x}$ |
3.已知抛物线C:y2=4x的交点为F,直线y=x-1与C相交于A,B两点,与双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=2(a>0,b>0)的渐近线相交于M,N两点,若线段AB与MN的中点相同,则双曲线E离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
13.若等差数列{an}的公差为d,前n项和为Sn,记bn=$\frac{{S}_{n}}{n}$,则( )
| A. | 数列{bn}是等差数列,{bn}的公差也为d | |
| B. | 数列{bn}是等差数列,{bn}的公差为2d | |
| C. | 数列{an+bn}是等差数列,{an+bn}的公差为d | |
| D. | 数列{an-bn}是等差数列,{an-bn}的公差为$\frac{d}{2}$ |
17.双曲线x2-$\frac{{y}^{2}}{4}$=1的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |