双曲线x2-$\frac{{y}^{2}}{4}$=1的离心率为( )A．$\frac{\sqrt{3}}{2}$B．$\sqrt{3}$C．$\frac{\sqrt{5}}{2}$D．$\sqrt{5}$ 题目和参考答案——青夏教育精英家教网——

题目内容

17．双曲线x²-$\frac{{y}^{2}}{4}$=1的离心率为（　　）

A．

$\frac{\sqrt{3}}{2}$

B．

$\sqrt{3}$

C．

$\frac{\sqrt{5}}{2}$

D．

$\sqrt{5}$

分析直接利用双曲线方程，求出实轴长以及焦距的长，即可得到双曲线的离心率．

解答解：双曲线x²-$\frac{{y}^{2}}{4}$=1的实轴长为：2，焦距的长为：2$\sqrt{1+4}$=2$\sqrt{5}$，
双曲线的离心率为：e=$\frac{2c}{2a}$=$\frac{2\sqrt{5}}{2}$=$\sqrt{5}$．
故选：D．

点评本题考查双曲线的简单性质的应用，是基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

4．已知向量$\overrightarrow{a}$=（3，-1），|$\overrightarrow{b}$|=$\sqrt{5}$，$\overrightarrow{a}$$•\overrightarrow{b}$=-5，$\overrightarrow{c}$=x$\overrightarrow{a}$+（1-x）$\overrightarrow{b}$．
（Ⅰ）若$\overrightarrow{a}$$⊥\overrightarrow{c}$，求实数x的值；
（Ⅱ）当|$\overrightarrow{c}$|取最小值时，求$\overrightarrow{b}$与$\overrightarrow{c}$的夹角的余弦值．

8．下列命题中错误的个数为：（　　）
①y=$\frac{1}{2}+\frac{1}{{{2^x}-1}}$的图象关于（0，0）对称；
②y=x³+x+1的图象关于（0，1）对称；
③y=$\frac{1}{{{x^2}-1}}$的图象关于直线x=0对称；
④y=sinx+cosx的图象关于直线x=$\frac{π}{4}$对称．

5．已知函数$f（x）=1-2{sin^2}（x+\frac{π}{8}）+2sin（x+\frac{π}{8}）cos（x+\frac{π}{8}）$．
（1）求f（x）的最小正周期及单调增区间；
（2）求f（x）在区间$[{-\frac{π}{4}，\frac{3π}{8}}]$上的最值．

12．设函数f（x）=2x³+3ax²+3bx+c在x=1及x=2时取得极值，且函数y=f（x）过原点，求函数y=f（x）的表达式．

2．在△ABC中，角A，B，C所对的边分别为a，b，c，若2cos2B=4cosB-3
（Ⅰ）求角B的大小
（Ⅱ）若S_△ABC=$\sqrt{3}$，asinA+csinC=5sinB，求边b．

9．设f_n（x）是等比数列1，-x，x²，…，（-x）ⁿ的各项和，则f₂₀₁₆（2）等于（　　）

$\frac{{{2^{2016}}+1}}{3}$

$\frac{{{2^{2016}}-1}}{3}$

$\frac{{{2^{2017}}+1}}{3}$

$\frac{{{2^{2017}}-1}}{3}$

6．已知命题p：不等式x²-2ax-2a+3≥0恒成立；命题q：不等式x²+ax+2＜0有解．
（Ⅰ）若p∨q和￢q均为真命题，求实数a的取值范围；
（Ⅱ）若p是真命题，抛物线y=x²与直线y=ax+1相交于M，N两点，O为坐标原点，求△OMN面积的最大值．

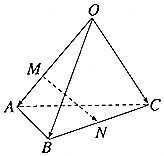如图，四面体OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且OM=2MA，N为BC的中点，$\overrightarrow{MN}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$，则x+y+z=$\frac{1}{3}$．