题目内容
15.已知直线l的极坐标方程为$\sqrt{3}ρcosθ+ρsinθ-1=0$,曲线C的极坐标方程为ρ=4.(1)将曲线C的极坐标方程化为普通方程;
(2)若直线l与曲线交于A,B两点,求线段AB 的长.
分析 (1)根据x=ρcosθ,y=ρsinθ以及ρ=x2+y2求出直线以及曲线C的普通方程即可;(2)根据点到直线的距离公式求出AB求出弦心距,从而求出弦长即可.
解答 解:(1)∵x=ρcosθ,y=ρsinθ以及ρ=x2+y2,
∴直线l的直角坐标方程为$\sqrt{3}x+y-1=0$
曲线C的直角坐标方程为x2+y2=16(4分)
(2)由(1)得:圆心(0,0)到直线的距离为$d=\frac{{|{\sqrt{3}×0+0-1}|}}{{\sqrt{3+1}}}=\frac{1}{2}$,
∴AB的长|AB|=$2\sqrt{{R^2}-{d^2}}=2\sqrt{16-\frac{1}{4}}=\sqrt{63}=3\sqrt{7}$(10分)
点评 本题考查了求曲线的普通方程,考查点到直线的距离公式,是一道中档题.

练习册系列答案
相关题目
5.函数f(x)=ln|x-1|+2cosπx(-2≤x≤4)的所有零点之和等于( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
6.若z•i=1-2i(i为虚数单位),则z的共轭复数是( )
| A. | -2-i | B. | 2-i | C. | 2+i | D. | -2+i |
3.在复平面内,复数${({1-\sqrt{2}i})^2}$对应的点P位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知x∈R,符号[x]表示不超过x的最大整数,如[1.9]=1,[2.01]=2.若函数$f(x)=\frac{x}{[x]}-m$(x≥1)有且仅有三个零点,则m的取值范围是( )
| A. | $[{\frac{3}{2},2}]$ | B. | $[{\frac{3}{2},2})$ | C. | $[{\frac{5}{4},\frac{4}{3}})$ | D. | $[{\frac{5}{4},\frac{4}{3}}]$ |
7.已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$一个周期的图象如图所示,则φ的值为( )
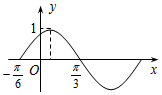

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{8}$ |