题目内容

13．设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、右焦点，P为椭圆上任一点，点M的坐标为（3，1），则|PM|+|PF1|的最小值为9．

分析 由题意可知：|PF1|+|PF2|=2a=10，|MF2|=1，|PM|≥|PF2|-|MF2|，|PM|+|PF1|≥|PF2|-|MF2|+|PF1|≥10-1=9，即可求得|PM|+|PF1|的最小值．

解答 解：由题意可知：a=5，b=4，c=3，F2（3，0），
连结PF2、MF2，如图，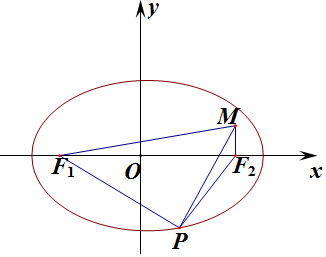

则|PF1|+|PF2|=2a=10，
|MF2|=1，
∵|PM|≥|PF2|-|MF2|，
∴|PM|+|PF1|≥|PF2|-|MF2|+|PF1|≥10-1=9，
∴|PM|+|PF1|的最小值9，
故答案为：9．

点评 本题考查椭圆的标准方程及简单几何性质，考查三角形的性质，考查计算能力，属于基础题．

练习册系列答案
相关题目
3．在复平面内，复数${（{1-\sqrt{2}i}）^2}$对应的点P位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
4．已知向量$\overrightarrow{a}$=（3，-1），|$\overrightarrow{b}$|=$\sqrt{5}$，$\overrightarrow{a}$$•\overrightarrow{b}$=-5，$\overrightarrow{c}$=x$\overrightarrow{a}$+（1-x）$\overrightarrow{b}$．
（Ⅰ）若$\overrightarrow{a}$$⊥\overrightarrow{c}$，求实数x的值；
（Ⅱ）当|$\overrightarrow{c}$|取最小值时，求$\overrightarrow{b}$与$\overrightarrow{c}$的夹角的余弦值．
1．已知函数f（x）=ex-ax，（e为自然对数的底数）．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若对任意实数x恒有f（x）≥0，求实数a的取值范围．
8．某产品的广告费用x（万元）与销售额y（万元）的统计数据如下表所示，根据表中的数据可得回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，其中$\widehat{a}$=0，据此模型预报，当广告费用为7万元时的销售额为（　　）
x4235
y38203151
A．60B．70C．73D．69
1．设a≠0，函数f（x）=$\left\{\begin{array}{l}4{log_2}（-x），x＜0\\|{{x^2}+ax}|，x≥0\end{array}$，若$f（f（-\sqrt{2}））=4$，则f（a）等于（　　）
A．8B．4C．2D．1
8．下列命题中错误的个数为：（　　）
①y=$\frac{1}{2}+\frac{1}{{{2^x}-1}}$的图象关于（0，0）对称；
②y=x3+x+1的图象关于（0，1）对称；
③y=$\frac{1}{{{x^2}-1}}$的图象关于直线x=0对称；
④y=sinx+cosx的图象关于直线x=$\frac{π}{4}$对称．
A．0B．1C．2D．3
5．已知函数$f（x）=1-2{sin^2}（x+\frac{π}{8}）+2sin（x+\frac{π}{8}）cos（x+\frac{π}{8}）$．
（1）求f（x）的最小正周期及单调增区间；
（2）求f（x）在区间$[{-\frac{π}{4}，\frac{3π}{8}}]$上的最值．
6．已知命题p：不等式x2-2ax-2a+3≥0恒成立；命题q：不等式x2+ax+2＜0有解．
（Ⅰ）若p∨q和￢q均为真命题，求实数a的取值范围；
（Ⅱ）若p是真命题，抛物线y=x2与直线y=ax+1相交于M，N两点，O为坐标原点，求△OMN面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网