题目内容

16．若函数f（x）=x2+2xf'（2）+lnx，则f'（2）等于（　　）
A．-2B．2C．-$\frac{9}{2}$D．$\frac{9}{2}$

分析 求出函数的导数，然后赋值求解即可．

解答 解：函数f（x）=x2+2xf'（2）+lnx，
可得f′（x）=2x+2f′（2）+$\frac{1}{x}$，
∴f′（2）=4+2f′（2）+$\frac{1}{2}$，
∴f′（2）=-$\frac{9}{2}$
故选：C

点评 本题考查导数的运算法则，考查计算能力，属于基础题．

练习册系列答案
相关题目
11．下列函数中为奇函数的是（　　）
A．y=x2+2xB．y=ln|x|C．y=（$\frac{1}{3}$）xD．y=xcosx
12．已知函数f（x）=$\left\{\begin{array}{l}{-\frac{3x+2}{x+1}，x∈（-1，0]}\\{x，x∈（0，1]}\end{array}\right.$且g（x）=mx+m，若g（x）=f（x）在（-1，1]内有且仅有两个不同的根，则实数m的取值范围是（　　）
A．（-$\frac{9}{4}$，-2]∪（0，$\frac{1}{2}$]B．（-$\frac{11}{4}$，-2]∪（0，$\frac{1}{2}$]C．（-$\frac{9}{4}$，-2]∪（0，$\frac{2}{3}$]D．（-$\frac{11}{4}$，-2]∪（0，$\frac{2}{3}$]
4．（1）已知数列{an}是等差数列，且${a_1}+{a_5}+{a_9}=\frac{π}{4}$，求$sin（{{a_4}+{a_6}+\frac{2017π}{2}}）$的值；
（2）已知数列{an}是等差数列，且满足${a_2}^2={a_1}{a_5}，{a_1}+{a_2}+{a_5}=26$，求数列{an}的 通项公式．
11．已知向量$\vec a=（1，cos2x），\vec b=（sin2x，-\sqrt{3}）$，函数f（x）=$\overrightarrow a•\overrightarrow b$．
（1）求函数f（x）的单调增区间；
（2）若$f（{\frac{θ}{2}+\frac{2π}{3}}）=\frac{6}{5}$，求cos2θ的值．
1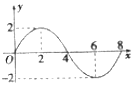．已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，x≥0）的部分图象如图所示，则f（1）+f（2）+f（3）+…+f（11）的值等于（　　）
A．2B．$2+\sqrt{2}$C．$2+2\sqrt{2}$D．$-2-\sqrt{2}$
8．若集合A={x|-3＜x＜2}，B={x|0＜x＜3}，则A∩B=（　　）
A．{x|-3＜x＜0}B．{x|-3＜x＜3}C．{x|0＜x＜2}D．{x|0＜x＜3}
5．设0≤x＜2π，且$\sqrt{1-sin2x}$=sinx-cosx，则x的取值范围是$[\frac{π}{4}，\frac{5π}{4}]$．
6．4个男生，3个女生站成一排．（必须写出算式再算出结果才得分）
（Ⅰ）3个女生必须排在一起，有多少种不同的排法？
（Ⅱ）任何两个女生彼此不相邻，有多少种不同的排法？
（Ⅲ）甲乙二人之间恰好有三个人，有多少种不同的排法？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网