题目内容
8．若集合A={x|-3＜x＜2}，B={x|0＜x＜3}，则A∩B=（ ）| A． | {x|-3＜x＜0} | B． | {x|-3＜x＜3} | C． | {x|0＜x＜2} | D． | {x|0＜x＜3} |
分析 找出A与B解集的公共部分，即可确定出两集合的交集．
解答 解：∵集合A={x|-3＜x＜2}，B={x|0＜x＜3}，
∴A∩B={x|0＜x＜2}．
故选：C
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
3．函数y=lg（cosx-$\frac{\sqrt{3}}{2}$）的定义域为（ ）
| A． | （-$\frac{π}{6}$，$\frac{π}{6}$） | B． | （kπ-$\frac{π}{6}$，kπ+$\frac{π}{6}$）（k∈π） | ||
| C． | （2kπ-$\frac{π}{6}$，2kπ+$\frac{π}{6}$）（k∈Z） | D． | R |
4．有这样一段演绎推理：“指数函数y=ax（a＞0且a≠1）是增函数，而y=（$\frac{1}{2}$）x是指数函数，所以y=（$\frac{1}{2}$）x是增函数”．上面推理显然是错误的，是因为（ ）
| A． | 大前提错导致结论错 | B． | 小前提错导致结论错 | ||
| C． | 推理形式错导致结论错 | D． | 大前提和小前提错导致结论错 |
16．若函数f（x）=x2+2xf'（2）+lnx，则f'（2）等于（ ）
| A． | -2 | B． | 2 | C． | -$\frac{9}{2}$ | D． | $\frac{9}{2}$ |
如图，四边形ABCD是边长为1的正方形，ED⊥平面ABCD，FB∥ED，且ED=FB=1，G为BC的中点．
20．
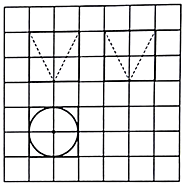如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）| A． | $20+\sqrt{5}π$ | B． | $24+\sqrt{5}π$ | C． | $20+（\sqrt{5}-1）π$ | D． | $24+（\sqrt{5}-1）π$ |
17．已知复数z=x+（x-a）i，若对任意实数x∈（1，2），恒有|z|＞|$\overline{z}$+i|，则实数a的取值范围为（ ）
| A． | （-∞，$\frac{1}{2}$] | B． | （-∞，$\frac{1}{2}$） | C． | [$\frac{3}{2}$，+∞） | D． | （$\frac{3}{2}$，+∞） |