题目内容
5.设0≤x<2π,且$\sqrt{1-sin2x}$=sinx-cosx,则x的取值范围是$[\frac{π}{4},\frac{5π}{4}]$.分析 利用二倍角公式将已知等式左边被开方数利用同角三角函数间的基本关系变形后,利用完全平方公式化简,再利用二次根式的化简公式变形,得到sinx大于等于cosx,由x的范围,利用正弦及余弦函数图象即可得出x的范围.
解答 解:∵$\sqrt{1-sin2x}$=$\sqrt{si{n}^{2}x-2sinxcosx+co{s}^{2}x}$=$\sqrt{(sinx-cosx)^{2}}$=|sinx-cosx|=sinx-cosx,
∴sinx-cosx≥0,即sinx≥cosx,
∵0≤x≤2π,
∴x的取值范围是$\frac{π}{4}$≤x≤$\frac{5π}{4}$.
故答案为:$[\frac{π}{4},\frac{5π}{4}]$.
点评 本题考查了同角三角函数间的基本关系,完全平方公式的运用,二次根式的化简公式,以及正弦、余弦函数的图象与性质,将已知等式进行适当的变形是解本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
16.若函数f(x)=x2+2xf'(2)+lnx,则f'(2)等于( )
| A. | -2 | B. | 2 | C. | -$\frac{9}{2}$ | D. | $\frac{9}{2}$ |
20.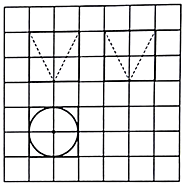 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | $20+\sqrt{5}π$ | B. | $24+\sqrt{5}π$ | C. | $20+(\sqrt{5}-1)π$ | D. | $24+(\sqrt{5}-1)π$ |
10.已知p:${log_2}({{x^2}-3x})>2$,q:$\frac{x-4}{x+1}>0$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知复数z=x+(x-a)i,若对任意实数x∈(1,2),恒有|z|>|$\overline{z}$+i|,则实数a的取值范围为( )
| A. | (-∞,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$) | C. | [$\frac{3}{2}$,+∞) | D. | ($\frac{3}{2}$,+∞) |
14.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
其中${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
附表
问能否有99%以上的把握认为爱好该项运动与性别有关?
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3,841 | 6.635 | 10.828 |
15.已知数列{an}是等比数列,a3=1,a5=4,则公比q等于( )
| A. | 2 | B. | -2 | C. | $±\frac{1}{2}$ | D. | ±2 |
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.