题目内容
1.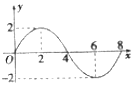 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+2\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
分析 根据图象求出函数f(x)=Asin(ωx+ϕ)的解析式和周期,即可求出f(1)+f(2)+f(3)+…+f(11)的值.
解答 解:由图象可知:A=2,T=8,
∴ω=$\frac{π}{4}$
函数f(x)=2sin($\frac{π}{4}x$+ϕ)
图象过(0,0),(2,2)
可得ϕ=0,
那么:函数f(x)=2sin($\frac{π}{4}x$).
根据正弦函数的性质和周期可得f(1)+f(2)+f(3)+…+f(8)=0.
那么f(1)+f(2)+f(3)+…+f(11)=f(9)+f(10)+f(11)
=2sin(2$π+\frac{π}{4}$)+2sin(2π$+\frac{π}{2}$)+2sin(2π$+\frac{3π}{4}$)=2$+2\sqrt{2}$.
故选C.
点评 本题考查了三角函数解析式的求法和正弦函数的性质和周期的运用,属于基础题.

练习册系列答案
相关题目
17.已知F1,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以F1F2为直径的圆与双曲线右支的一个交点为P,PF1与双曲线相交于Q,且|PQ|=2|QF1|,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
9.已知复数z满足(z-1)i=i+1,则z在复平面内所对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
16.若函数f(x)=x2+2xf'(2)+lnx,则f'(2)等于( )
| A. | -2 | B. | 2 | C. | -$\frac{9}{2}$ | D. | $\frac{9}{2}$ |
6.已知α∈($\frac{3}{2}$π,2π),且满足cos(α+$\frac{2017}{2}$π)=$\frac{3}{5}$,则sinα+cosα=( )
| A. | -$\frac{7}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{5}$ |
10.已知p:${log_2}({{x^2}-3x})>2$,q:$\frac{x-4}{x+1}>0$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.设p:0<x<2,q:2x>1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.