题目内容
曲线y=
x3-2在点(1,-
) 处切线的斜率为( )
| 1 |
| 3 |
| 5 |
| 3 |
A、
| ||
| B、1 | ||
| C、-1 | ||
D、-
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求曲线在某点处的切线的斜率,就是求曲线在该点处的导数值,先求导函数,然后将点的坐标代入即可求得结果.
解答:
解:y=
x3-2的导数为:y′=x2,
将点(1,-
)的横坐标代入,即可得斜率为:k=1.
故选:B.
| 1 |
| 3 |
将点(1,-
| 5 |
| 3 |
故选:B.
点评:本题考查了导数的几何意义,它把函数的导数与曲线的切线联系在一起,使导数成为函数知识与解析几何知识交汇的一个重要载体,属于基础题.

练习册系列答案
相关题目
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
| A、36种 | B、30种 |
| C、24种 | D、6种 |
若{an}为等差数列,Sn是其前n项和,且S11=
,则tana6=( )
| 88π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
如图程序的功能是( )


| A、统计十个数据中负数的个数 |
| B、找出十个数据中的负数 |
| C、判断x的符号 |
| D、求十个数据中所有负数的和 |
一个几何体的三视图及尺寸如图所示,则该几何体的体积为( )
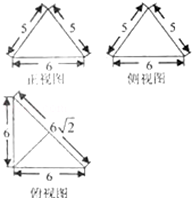

| A、48 | B、72 | C、12 | D、24 |
若数列{an}满足a1=2且an+an-1=2n+2n-1,Sn为数列{an}的前n项和,则log2(S2012+2)等于( )
| A、2013 | B、2012 |
| C、2011 | D、2010 |
函数y=2x+sinx的单调增区间是( )
| A、(-∞,+∞) | ||||
| B、(0,+∞) | ||||
C、(2kπ-
| ||||
| D、以上答案均不正确 |