题目内容
已知函数f(x)=ex-1,g(x+1)=-x2+2x,若f(a)=g(b),则b的取值范围是( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
考点:指数函数综合题
专题:函数的性质及应用
分析:利用换元法求出g(x)的表达式,根据函数的性质求出相应的取值范围,建立条件关系即可得到结论.
解答:
解:∵g(x+1)=-x2+2x,
∴设t=x+1,则x=t-1,
∴g(t)=-(t-1)2+2(t-1)=-t2+4t-3,
∴g(x)=-x2+4x-3=-(x-2)2+1≤1,f(x)=ex-1≥-1,
若有f(a)=g(b),
则g(b)∈(-1,1],
即-b+24b-3>-1,
即 b2-4b+2<0,
解得2-
<b<2+
.
即实数b的取值范围为(2-
,2+
),
故选B.
∴设t=x+1,则x=t-1,
∴g(t)=-(t-1)2+2(t-1)=-t2+4t-3,
∴g(x)=-x2+4x-3=-(x-2)2+1≤1,f(x)=ex-1≥-1,
若有f(a)=g(b),
则g(b)∈(-1,1],
即-b+24b-3>-1,
即 b2-4b+2<0,
解得2-
| 2 |
| 2 |
即实数b的取值范围为(2-
| 2 |
| 2 |
故选B.
点评:本题主要考查函数与方程之间的关系,利用换元法求出函数g(x)的表达式是解决本题的关键,考查学生的推理运算能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
若x>1,则函数y=
+x的最小值是( )
| 1 |
| x-1 |
| A、3 | B、4 | C、2 | D、8 |
设动点P(x,y)满足
,则z=x-y的最小值是( )
|
| A、2 | B、-4 | C、-1 | D、4 |
f(a)=a3-2a+1,求f(2)=( )
| A、3 | B、4 | C、5 | D、2 |
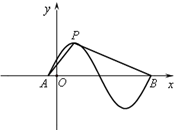 函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-
函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-