题目内容
20.函数y=2x+1的反函数是( )| A. | y=logx2+1,x>0且x≠1 | B. | y=log2x+1,x>0 | ||
| C. | y=log2x-1,x>0 | D. | y=log2(x-1),x>1 |
分析 将y=2x+1作为方程利用指数式和对数式的互化解出x,然后确定原函数的值域即得反函数的定义域,从而求出所求.
解答 解:由y=2x+1得x=log2(y-1)且y>1
即:y=log2(x-1),x>1
所以函数y=2x+1的反函数是y=log2(x-1)(x>1)
故选D.
点评 本题主要考查了反函数,以及指数式与对数式的互化,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
12.${∫}_{0}^{π}$(cosx+2)dx等于( )
| A. | 2π | B. | 0 | C. | π+2 | D. | 1 |
15.已知圆C:(x-1)2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4(m∈R),则直线l过的定点及直线与圆相交得的最短弦长分别为( )
| A. | (3,1),$4\sqrt{5}$ | B. | (2,1),$4\sqrt{5}$ | C. | (-3,1),$4\sqrt{3}$ | D. | (2,-1),3$\sqrt{3}$ |
5.方程${2^{{{log}_3}x}}=\frac{1}{4}$的解为( )
| A. | 9 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{9}$ |
12.在△ABC中,三个内角∠A,∠B,∠C所对的边分别为a,b,c,且A:B:C=1:2:3,则a:b:c=( )
| A. | 3:2:1 | B. | 2:$\sqrt{3}$:1 | C. | 1:2:3 | D. | 1:$\sqrt{3}$:2 |
10.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>1}\\{(\frac{1}{2})^{x},x≤1}\end{array}\right.$,则f(f(-$\frac{1}{2}$))=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
 已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.
已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.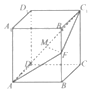 已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,且四边形ABCD为菱形,F为棱BB1的中点,N为线段AC1的中点.
已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,且四边形ABCD为菱形,F为棱BB1的中点,N为线段AC1的中点.