题目内容
12．在△ABC中，三个内角∠A，∠B，∠C所对的边分别为a，b，c，且A：B：C=1：2：3，则a：b：c=（ ）| A． | 3：2：1 | B． | 2：$\sqrt{3}$：1 | C． | 1：2：3 | D． | 1：$\sqrt{3}$：2 |
分析 根据三角形的内角和定理，可判断此三角形为直角三角形，再利用30°所对的直角边是斜边的一半，勾股定理求解．
解答 解：∵∠A：∠B：∠C=1：2：3，
∴∠A=30°，∠B=60°，∠C=90°．
设a=x，则c=2x，
根据勾股定理，得b=$\sqrt{3}$x，
∴a：b：c=1：$\sqrt{3}$：2．
故选：D．
点评 本题主要考查了三角形内角和定理，勾股定理在解三角形中的应用，注意这一结论：30°的直角三角形中，三边从小到大的比是1：$\sqrt{3}$：2，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．函数y=2x+1的反函数是（ ）
| A． | y=logx2+1，x＞0且x≠1 | B． | y=log2x+1，x＞0 | ||
| C． | y=log2x-1，x＞0 | D． | y=log2（x-1），x＞1 |
17．设全集U=R，若集合A={x|$\frac{x-1}{4-x}$≥0}，B={x|log2x≤2}，则A∩B=（ ）
| A． | {x|x＜4} | B． | {x|x≤4} | C． | {x|1≤x＜4} | D． | {x|1≤x≤4} |
4．若抛物线y=$\frac{1}{4}$x2上一点P到焦点F的距离为5，则P点的坐标是（ ）
| A． | （4，±4） | B． | （±4，4） | C． | （±$\frac{79}{16}$，$\frac{\sqrt{79}}{8}$） | D． | （±$\frac{\sqrt{79}}{8}$，$\frac{79}{16}$） |
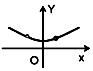
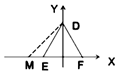如图所示，△DEF中，已知DE=DF，点M在直线EF上从左到右运动（点M不与E、F重合），对于M的每一个位置（x，0），记△DEM的外接圆面积与△DMF的外接圆面积的比值为f（x），那么函数y=f（x）的大致图象为（ ）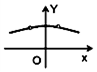
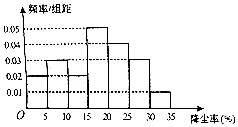空气质量问题，全民关注，有需求就有研究，某科研团队根据工地常用高压水枪除尘原理，制造了雾霾神器---雾炮，虽然雾炮不能彻底解决问题，但是能在一定程度上起到防霾、降尘的作用，经过测试得到雾炮降尘率的频率分布直方图：