题目内容
15.已知圆C:(x-1)2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4(m∈R),则直线l过的定点及直线与圆相交得的最短弦长分别为( )| A. | (3,1),$4\sqrt{5}$ | B. | (2,1),$4\sqrt{5}$ | C. | (-3,1),$4\sqrt{3}$ | D. | (2,-1),3$\sqrt{3}$ |
分析 (1)通过直线l转化为直线系,求出直线恒过的定点;
(2)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出m的值,再由勾股定理即可得到最短弦长.
解答 解(1):将直线化为直线束方程:x+y-4+(2x+y-7)=0.
联立方程x+y-4=0与2x+y-7=0,得点(3,1);
将点(3,1)代入直线方程,不论m为何值时都满足方程,所以直线l恒过定点(3,1);
(2)当直线l垂直于圆心与定点(3,1)所在直线时弦长最短,
斜率为2,代入方程得m=-$\frac{3}{4}$,此时直线l方程为2x-y-5=0,圆心到直线的距离为$\sqrt{5}$,
所以最短弦长为4$\sqrt{5}$;
故选:A.
点评 本题考查直线系方程的应用,考查直线与圆的位置关系,考查平面几何知识的运用,考查计算能力,属于中档题.

练习册系列答案
相关题目
6.若$tan({θ+\frac{π}{4}})=-3$,则2sin2θ-cos2θ=( )
| A. | $-\frac{6}{5}$ | B. | $-\frac{7}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
20.函数y=2x+1的反函数是( )
| A. | y=logx2+1,x>0且x≠1 | B. | y=log2x+1,x>0 | ||
| C. | y=log2x-1,x>0 | D. | y=log2(x-1),x>1 |
4.若抛物线y=$\frac{1}{4}$x2上一点P到焦点F的距离为5,则P点的坐标是( )
| A. | (4,±4) | B. | (±4,4) | C. | (±$\frac{79}{16}$,$\frac{\sqrt{79}}{8}$) | D. | (±$\frac{\sqrt{79}}{8}$,$\frac{79}{16}$) |
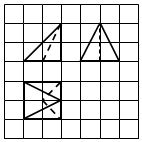 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为2.
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为2.