Question

把半径为r的四个小球全部放入一个大球内，则大球半径的最小值为

 

．

Answer 1

考点：球的体积和表面积

专题：空间位置关系与距离

分析：当四个小球彼此相外切，与大球内切时，大球半径的最小，此时四个小球的球心为边长为2r的正四面体的四个顶点，大球半径的最小值为正四面体外接球半径加小球半径．

解答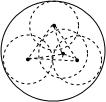： 解：当四个小球彼此相外切，与大球内切时，大球半径的最小，
如图所示：
四个小球，三个在下，一个在上，四个球心连线成正四面体，
该正四面体的边长为2r，
则正四面体的高为

2 6

3

r，
则正四面体的外接球半径为

6

2

r，
∴大球半径最小为：（1+

6

2

）r，
故答案为：（1+

6

2

）r

点评：本题考查的知识点是球的体积与表面积，其中分析出当四个小球彼此相外切，与大球内切时，大球半径的最小，是解答的关键．