题目内容
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(2)在(1)的条件下,当x为何值时,本年度的年利润最大?最大利润为多少?
(1)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(2)在(1)的条件下,当x为何值时,本年度的年利润最大?最大利润为多少?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)根据年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.可设年利润为y,从而可以构建函数关系式;
(2)利用二次函数求最值的方法可得结论.
(2)利用二次函数求最值的方法可得结论.
解答:
解:(1)由题意,设年利润为y,则有
y=[13(1+0.7x)-10×(1+x)]×5000(1+0.4x)=5000(-0.36x2+0.3x+3),(0<x<1)…(6分)
由5000(-0.36x2+0.3x+3)>3×5000,得0<x<
…(9分)
(2)本年度利润为y=5000(-0.36x2+0.3x+3)…(11分)
当x=
时,y有最大值为15312.5(万元) …(13分)
答:(1)投入成本增加的比例x的范围是0<x<
;(2)当x=
时,本年度的年利润最大,是15312.5万元. …(15分)
y=[13(1+0.7x)-10×(1+x)]×5000(1+0.4x)=5000(-0.36x2+0.3x+3),(0<x<1)…(6分)
由5000(-0.36x2+0.3x+3)>3×5000,得0<x<
| 5 |
| 6 |
(2)本年度利润为y=5000(-0.36x2+0.3x+3)…(11分)
当x=
| 5 |
| 12 |
答:(1)投入成本增加的比例x的范围是0<x<
| 5 |
| 6 |
| 5 |
| 12 |
点评:本题的考点是函数模型的选择与应用,主要考查二次函数模型的构建,关键是利用年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x2-cosx,设a=f(-0.5),b=f(0),c=f(3),则( )
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<a<c |
现有5名同学去听同时进行的6个课外知识讲座,每名同学可自由选择其中的一个讲座,不同选法的种数是( )
| A、54 | ||
| B、65 | ||
C、
| ||
| D、6×5×4×3×2 |
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.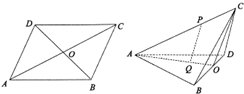 如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.
如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.