题目内容
现有5名同学去听同时进行的6个课外知识讲座，每名同学可自由选择其中的一个讲座，不同选法的种数是（ ）
| A、54 | ||
| B、65 | ||
C、
| ||
| D、6×5×4×3×2 |
考点：计数原理的应用
专题：排列组合
分析：5名同学去听同时进行的6个课外知识讲座，实际上是有6个人选择座位，且每人有6种选择方法，根据分步计数原理得到结果．
解答：
解：∵每位同学均有6种讲座可选择，
∴5位同学共有6×6×6×6×6=65种，
故选：B．
∴5位同学共有6×6×6×6×6=65种，
故选：B．
点评：本题考查分步计数原理，解题的关键是看清题目的实质，分步乘法计数原理：首先确定分步标准，其次满足：必须并且只需连续完成这n个步骤，这件事才算完成．
练习册系列答案
活力课时同步练习册系列答案
相关题目
设z为复数，“z=i”是“z2+1=0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
已知F是双曲线
-
=1（a＞0，b＞0）的左焦点，E是该双曲线的右顶点，过点F且垂直于x轴的直线与双曲线交于A、B两点，点E在以AB为直径的圆内，则该双曲线的离心率e的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，+∞） | ||
| B、（1，2） | ||
C、（1，1+
| ||
| D、（2，+∞） |
已知二次函数f（x）=4x2-2（p-2）x-2p2-p+1，若在[-1，1]上存在x使得f（x）＞0，则实数p的取值范围是（ ）
A、[-
| ||||
| B、[1，3] | ||||
C、[-
| ||||
D、（-3，
|
用”辗转相除法”求得98与63的最大公约数是（ ）
| A、17 | B、14 | C、9 | D、7 |
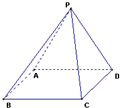如图，用四种不同的颜色给图中的P、A、B、C、D五个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共有（ ）种．| A、72 | B、86 |
| C、106 | D、120 |
如图，我国某搜救舰艇以30（海里/小时）的速度在南海某区域搜索，在点A处测得基地P在南偏东60°，向北航行40分钟后到达点B，测得基地P在南偏东30°，并发现在北偏东60°的航向上有疑似马航飘浮物，搜救舰艇立即转向直线前往，再航行80分钟到达飘浮物C处，求此时P、C间的距离．