题目内容
已知(
+3x2)n展开式各项系数的和比它的二项式系数的和大992.
(Ⅰ)求n;
(Ⅱ)求展开式中x6的项;
(Ⅲ)求展开式系数最大项.
| 3 | x2 |
(Ⅰ)求n;
(Ⅱ)求展开式中x6的项;
(Ⅲ)求展开式系数最大项.
考点:二项式系数的性质
专题:二项式定理
分析:(Ⅰ)由题意可得 (1+3)n-2n=992,由此求得n的值.
(Ⅱ)在展开式的通项公式中,令x的幂指数等于6,求得r的值,可得展开式中x6的项.
(Ⅲ)设展开式系数最大项为第r+1项,则有
,求得r的值,可得结论.
(Ⅱ)在展开式的通项公式中,令x的幂指数等于6,求得r的值,可得展开式中x6的项.
(Ⅲ)设展开式系数最大项为第r+1项,则有
|
解答:
解:(Ⅰ)由题意可得 (1+3)n-2n=992,即(2n-32)(2n+31)=0,解得 n=5.
(Ⅱ)(
+3x2)n=(
+3x2)5展开式的通项公式为Tr+1=
•3r•x
,
令
=6,求得r=2,故开式求展开式中x6的项为
×9•x6=90x6.
(Ⅲ)设展开式系数最大项为第r+1项,则有
,
解得r=4,故第5项的系数最大为
•34 x
=405x
.
(Ⅱ)(
| 3 | x2 |
| 3 | x2 |
| C | r 5 |
| 10+4r |
| 3 |
令
| 10+4r |
| 3 |
| C | 2 5 |
(Ⅲ)设展开式系数最大项为第r+1项,则有
|
解得r=4,故第5项的系数最大为
| C | 4 5 |
| 26 |
| 3 |
| 26 |
| 3 |
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
△ABC中,已知a=5
,c=10,A=30°,则C=( )
| 2 |
| A、45° | B、60° |
| C、135° | D、45°或135° |
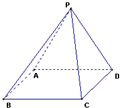 如图,用四种不同的颜色给图中的P、A、B、C、D五个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有( )种.
如图,用四种不同的颜色给图中的P、A、B、C、D五个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有( )种.| A、72 | B、86 |
| C、106 | D、120 |
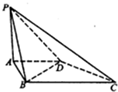 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.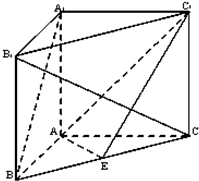 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.