题目内容
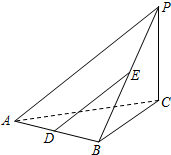
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.(1)求证:DE∥平面PAC;
(2)求证:AB⊥PB;
(3)求点C到平面ABP的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:计算题,空间位置关系与距离
分析:(1)由D,E分别是AB,PB的中点,结合三角形中位线定理和线面平行的判定定理可得DE∥平面PAC;
(2)由线面垂直的性质,可得PC⊥AB,结合AB⊥BC和线面垂直的判定定理可得AB⊥平面PBC,再由线面垂直的性质可得AB⊥PB;
(3)点C到平面PAB的距离为h,由等体积法得:VC-PAB=VP-ABC,即可求点C到平面ABP的距离.
(2)由线面垂直的性质,可得PC⊥AB,结合AB⊥BC和线面垂直的判定定理可得AB⊥平面PBC,再由线面垂直的性质可得AB⊥PB;
(3)点C到平面PAB的距离为h,由等体积法得:VC-PAB=VP-ABC,即可求点C到平面ABP的距离.
解答:
 (1)证明:∵D,E分别是AB,PB的中点,∴DE∥AP. …(2分)
(1)证明:∵D,E分别是AB,PB的中点,∴DE∥AP. …(2分)
∵AP?平面PAC,且DE?平面PAC,
∴DE∥平面PAC …(5分)
(2)证明:∵PC⊥平面ABC,AB?平面ABC,
∴PC⊥AB …(7分)
∵AB⊥BC,且PC∩BC=C,PC、BC?平面PBC,
∴AB⊥平面PBC------------(9分)
∵PB?平面PBC,∴AB⊥PB------------(10分)
(3)解:∵PC⊥平面ABC,BC?平面ABC,
∴PC⊥BC
在Rt△PBC中,由勾股定理得PB2=PC2+BC2=12+12=2,∴PB=
…(11分)
由(2)证知△PAB是直角三角形,
设点C到平面PAB的距离为h,由等体积法得:VC-PAB=VP-ABC
即
S△PAB•h=
S△ABC•PC,∴h=
=
=
=
=
即点C到平面PAB的距离为
.…(14分)
 (1)证明:∵D,E分别是AB,PB的中点,∴DE∥AP. …(2分)
(1)证明:∵D,E分别是AB,PB的中点,∴DE∥AP. …(2分)∵AP?平面PAC,且DE?平面PAC,
∴DE∥平面PAC …(5分)
(2)证明:∵PC⊥平面ABC,AB?平面ABC,
∴PC⊥AB …(7分)
∵AB⊥BC,且PC∩BC=C,PC、BC?平面PBC,
∴AB⊥平面PBC------------(9分)
∵PB?平面PBC,∴AB⊥PB------------(10分)
(3)解:∵PC⊥平面ABC,BC?平面ABC,
∴PC⊥BC
在Rt△PBC中,由勾股定理得PB2=PC2+BC2=12+12=2,∴PB=
| 2 |
由(2)证知△PAB是直角三角形,
设点C到平面PAB的距离为h,由等体积法得:VC-PAB=VP-ABC
即
| 1 |
| 3 |
| 1 |
| 3 |
| S△ABC•PC |
| S△PAB |
| ||
|
| BC•PC |
| PB |
| 1×1 | ||
|
| ||
| 2 |
即点C到平面PAB的距离为
| ||
| 2 |
点评:本题考查直线与平面平行的判定,直线与平面垂直的性质,考查点到平面的距离,解答的关键是熟练掌握空间线面关系的判定定理及性质,属于中档题.

练习册系列答案
相关题目
已知f(x)是定义在R上的函数,f(-x)=f(x)且f(x)=f(x+2),当0≤x≤1时,f(x)=x2,若方程f(x)=x+a有两个不等实根,那么实数a的值为( )
A、2k或2k-
| ||
B、k或k-
| ||
| C、2k(k∈z) | ||
| D、k(k∈z) |
用”辗转相除法”求得98与63的最大公约数是( )
| A、17 | B、14 | C、9 | D、7 |
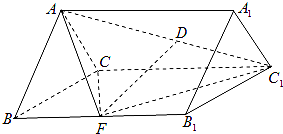 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.