题目内容
已知曲线C的极坐标方程是ρ=2
sinθ,以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)写出曲线C的普通方程,并说明它表示什么曲线;
(2)过点P(3,
)作倾斜角为α=
的直线L与曲线C相交于A,B两点,求线段AB的长度和|PA|•|PB|的值.
| 5 |
(1)写出曲线C的普通方程,并说明它表示什么曲线;
(2)过点P(3,
| 5 |
| 3π |
| 4 |
考点:参数方程化成普通方程,点的极坐标和直角坐标的互化
专题:坐标系和参数方程
分析:(1)根据极坐标和角坐标的互化公式把曲线C的极坐标方程化为直角坐标方程,从而得出结论.
(2)设直线l的参数方程是
(t是参数),代人曲线C的方程,化简并利用韦达定理、参数的几何意义求得线段AB的长度和|PA|•|PB|的值.
(2)设直线l的参数方程是
|
解答:
解:(1)曲线C的极坐标方程是ρ=2
sinθ,化为直角坐标方程为x2 +(y-
)2=5,
它是以(0,
)为圆心,半径为
的圆.
(2)设直线l的参数方程是
(t是参数),
代人x2+y2-2
y=0,得t2-3
t+4=0.
∵t1+t2=3
,t1•t2=4,
∴|AB|=
=
,|PA|•|PB|=4.
| 5 |
| 5 |
它是以(0,
| 5 |
| 5 |
(2)设直线l的参数方程是
|
代人x2+y2-2
| 5 |
| 2 |
∵t1+t2=3
| 2 |
∴|AB|=
| (t1+t2)2-4t1t2 |
| 2 |
点评:本题主要考查把极坐标方程、参数方程化为直角坐标返程的方法,韦达定理、参数的几何意义,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的面积是30,内角A,B,C所对边长分别为a,b,c,cosA=
,则
•
=( )
| 12 |
| 13 |
| AB |
| AC |
| A、60 | B、144 |
| C、72 | D、156 |
已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若在[-1,1]上存在x使得f(x)>0,则实数p的取值范围是( )
A、[-
| ||||
| B、[1,3] | ||||
C、[-
| ||||
D、(-3,
|
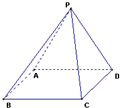 如图,用四种不同的颜色给图中的P、A、B、C、D五个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有( )种.
如图,用四种不同的颜色给图中的P、A、B、C、D五个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有( )种.| A、72 | B、86 |
| C、106 | D、120 |
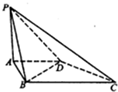 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.