题目内容
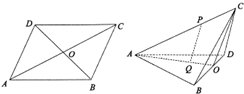 如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.
如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.(1)求证:PQ∥平面BCD;
(2)求证:PO⊥平面ABD;
(3)求BP与平面BCD所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由题意可得AQ=2QO,又AP=2PC,所以PQ∥CO,又PQ?平面BCD,CO?平面BCD,由线面平行的判定定理可得;
(2)易得OC=OA=2cos30°=
,在△AOC中,由余弦定理可得AC=3,在△PAO中,可得PO=1,由勾股定理可得PO⊥OA,又可得PO⊥BD,又AO∩BD=0,由线面垂直的判定可得;
(3)建立坐标系,求出
=(-1,0,1),平面BCD的法向量,利用向量的夹角公式,即可求出BP与平面BCD所成角的正弦值.
(2)易得OC=OA=2cos30°=
| 3 |
(3)建立坐标系,求出
| BP |
解答:
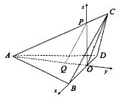 (1)证明:如图由ABCD为菱形,则AC⊥BD,∠AOC=120°,
(1)证明:如图由ABCD为菱形,则AC⊥BD,∠AOC=120°,
由Q为三角形ABD的重心,可得AQ=2QO,又AP=2PC,所以PQ∥CO,
又PQ?平面BCD,CO?平面BCD,所以PQ∥平面BCD;
(2)证明:由题意OC=OA=2cos30°=
,在△AOC中,由余弦定理可得
AC2=3+3-2×
×
×cos120°=9,所以AC=3,
又∠AOC=120°,AO=CO,∴∠PAO=30°,
在△PAO中,OA=
,AP=2,∠PAO=30°,所以PO=1,
所以PO2+OA2=AP2,所以PO⊥OA,
又BD⊥平面AOC,所以PO⊥BD,又AO∩BD=0,
所以PO⊥平面ABD;
(3)解:建立如图所示的坐标系,则B(1,0,0),D(-1,0,0),C(0,
,
),P(0,0,1),
∴
=(-1,0,1),
=(0,-
,-
),
=(-1,-
,-
),
设平面BCD的法向量为
=(x,y,z),则
,
取
=(0,-
,1),
设BP与平面BCD所成角为α,则sinα=|
|=
.
 (1)证明:如图由ABCD为菱形,则AC⊥BD,∠AOC=120°,
(1)证明:如图由ABCD为菱形,则AC⊥BD,∠AOC=120°,由Q为三角形ABD的重心,可得AQ=2QO,又AP=2PC,所以PQ∥CO,
又PQ?平面BCD,CO?平面BCD,所以PQ∥平面BCD;
(2)证明:由题意OC=OA=2cos30°=
| 3 |
AC2=3+3-2×
| 3 |
| 3 |
又∠AOC=120°,AO=CO,∴∠PAO=30°,
在△PAO中,OA=
| 3 |
所以PO2+OA2=AP2,所以PO⊥OA,
又BD⊥平面AOC,所以PO⊥BD,又AO∩BD=0,
所以PO⊥平面ABD;
(3)解:建立如图所示的坐标系,则B(1,0,0),D(-1,0,0),C(0,
| ||
| 2 |
| 3 |
| 2 |
∴
| BP |
| CB |
| ||
| 2 |
| 3 |
| 2 |
| CD |
| ||
| 2 |
| 3 |
| 2 |
设平面BCD的法向量为
| m |
|
取
| m |
| 3 |
设BP与平面BCD所成角为α,则sinα=|
| 1 | ||
|
| ||
| 4 |
点评:本题考查直线与平面平行的判定,以及直线与平面垂直的判定,考查线面角,正确运用向量法是关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离.
如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离.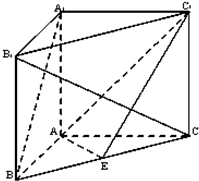 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.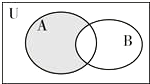 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.