题目内容
盒中装有6个零件,其中2个是使用过的,另外4个未经使用,
(1)从盒中随机一次抽取3个零件,求抽取到的3个零件中恰有1个是使用过的概率;
(2)从盒中每次随机抽取1个零件,观察后都将零件放回盒中,记3次抽取中抽到使用过的零件的次数为X,求X的分布列和数学期望.
(1)从盒中随机一次抽取3个零件,求抽取到的3个零件中恰有1个是使用过的概率;
(2)从盒中每次随机抽取1个零件,观察后都将零件放回盒中,记3次抽取中抽到使用过的零件的次数为X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(1)利用古典概型的概率公式,可求抽取到的3个零件中恰有1个是使用过的概率;
(2)确定随机变量X的所有取值,求出相应的概率,可得随机变量X的分布列和数学期望.
(2)确定随机变量X的所有取值,求出相应的概率,可得随机变量X的分布列和数学期望.
解答:
解:(1)记事件A为“抽取到3个零件中恰有一个是使用过的”,则 P(A)=
=
(2)依题有X~B(3,
),则
P(X=0)=(
)3=
,P(X=1)=
•
•(
)2=
,
P(X=2)=
•(
)2•
=
,P(X=3)=(
)3=
所以X的分布列如下
所以X的期望是EX=3×
=1
| ||||
|
| 3 |
| 5 |
(2)依题有X~B(3,
| 1 |
| 3 |
P(X=0)=(
| 2 |
| 3 |
| 8 |
| 27 |
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(X=2)=
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
| 1 |
| 27 |
所以X的分布列如下
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 3 |
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值,求出相应的概率.

练习册系列答案
相关题目
已知F是双曲线
-
=1(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,点E在以AB为直径的圆内,则该双曲线的离心率e的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,+∞) | ||
| B、(1,2) | ||
C、(1,1+
| ||
| D、(2,+∞) |
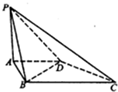 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2. 如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离.
如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离.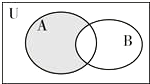 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.