题目内容
 如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l
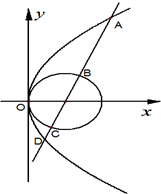
如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l交C1于A,D两点,交C2于B,C两点.
(Ⅰ)若|AB|+|CD|=2|BC|,求直线l的方程;
(Ⅱ)求|AB|•|CD|的值.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出抛物线的焦点为(1,0),圆的圆心为(1,0),半径为1.则圆心C2为抛物线的焦点,由|AB|+|CD|=2|BC|,得|AD|=3|BC|=6.设出直线l:y=k(x-1),联立抛物线方程消去y,得到二次方程,由根与系数的关系得到两根之和,又由抛物线的定义可得,|AD|=x1+x2+2,即可得到k,进而得到直线方程;
(Ⅱ)若l与x轴垂直,则x1=x2=1;若l与x轴不垂直,则有根与系数的关系,得到两根之积,再由抛物线的定义,即可得到所求的值.
(Ⅱ)若l与x轴垂直,则x1=x2=1;若l与x轴不垂直,则有根与系数的关系,得到两根之积,再由抛物线的定义,即可得到所求的值.
解答:
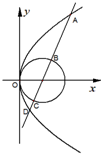 解:(Ⅰ)抛物线C1:y2=4x的焦点为(1,0),圆C2:(x-1)2+y2=1,
解:(Ⅰ)抛物线C1:y2=4x的焦点为(1,0),圆C2:(x-1)2+y2=1,
圆心为(1,0),半径为1.则圆心C2(1,0)为抛物线的焦点,
由|AB|+|CD|=2|BC|,得|AD|=3|BC|=6.
由题易得直线l的斜率存在且不为零,
设直线l:y=k(x-1),A(x1,y1),D(x2,y2),
由
,得k2x2-(2k2+4)x+k2=0,
则x1+x2=
,
又由抛物线的定义可得,|AD|=x1+x2+2=6,
所以x1+x2=
=4,解得k=±
,
则有直线l的方程为y=±
(x-1);
(Ⅱ)若l与x轴垂直,则x1=x2=1;
若l与x轴不垂直,则由(Ⅰ)知x1x2=
=1.
所以由抛物线的定义可得,|AB|•|CD|=(x1+1-1)(x2+1-1)=x1x2=1.
 解:(Ⅰ)抛物线C1:y2=4x的焦点为(1,0),圆C2:(x-1)2+y2=1,
解:(Ⅰ)抛物线C1:y2=4x的焦点为(1,0),圆C2:(x-1)2+y2=1,圆心为(1,0),半径为1.则圆心C2(1,0)为抛物线的焦点,
由|AB|+|CD|=2|BC|,得|AD|=3|BC|=6.
由题易得直线l的斜率存在且不为零,
设直线l:y=k(x-1),A(x1,y1),D(x2,y2),
由
|
则x1+x2=
| 2k2+4 |
| k2 |
又由抛物线的定义可得,|AD|=x1+x2+2=6,
所以x1+x2=
| 2k2+4 |
| k2 |
| 2 |
则有直线l的方程为y=±
| 2 |
(Ⅱ)若l与x轴垂直,则x1=x2=1;
若l与x轴不垂直,则由(Ⅰ)知x1x2=
| k2 |
| k2 |
所以由抛物线的定义可得,|AB|•|CD|=(x1+1-1)(x2+1-1)=x1x2=1.
点评:本题考查抛物线的定义、性质和方程的运用,考查直线与圆的位置关系,考查联立直线方程和抛物线方程,消去未知数,运用韦达定理解题,考查运算能力,属于中档题和易错题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
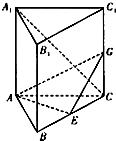 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.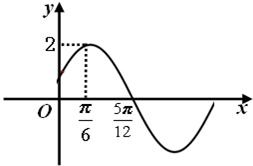 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<