题目内容
已知数列{an}的前n项和Sn=
n(n+1),bn是an与an+1的等差中项.
(Ⅰ)求bn;
(Ⅱ)设cn=
,数列{cn}的前n项和为Tn,若满足不等式bn+λ<Tn 的正整数n有且仅有两个,求实数λ的取值范围.
| 1 |
| 2 |
(Ⅰ)求bn;
(Ⅱ)设cn=
| 1 |
| (2n-1)bn |
考点:数列与不等式的综合,等差数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)先由数列{an}的前n项和Sn求an,然后利用等差中项求bn;
(Ⅱ)将bn=n+
代入cn求出cn=
-
,相邻项相消求出Tn,然后代入bn+λ<Tn 构造了函数f(n)=Tn-bn在(0,+∞)且n∈N*上是减函数,利用函数解题即可.
(Ⅱ)将bn=n+
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(Ⅰ)当n=1时,a1=1;当n≥2时,an=Sn-Sn-1=n;故an=n.
又bn 是an 与 an+1的等差中项,所以bn=
,得bn=n+
.
(Ⅱ)由(Ⅰ)得cn=
=
-
,
所以Tn=1-
.
设f(n)=Tn-bn=1-
-(n+
)=1-(n+
+
),则f(n)在(0,+∞)且n∈N*上是减函数.
因为满足不等式bn+λ<Tn 的正整数有且仅有两个,所以应满足
解得-
≤λ<-
.
又bn 是an 与 an+1的等差中项,所以bn=
| an+an+1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)得cn=
| 2 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=1-
| 1 |
| 2n+1 |
设f(n)=Tn-bn=1-
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
n+
|
因为满足不等式bn+λ<Tn 的正整数有且仅有两个,所以应满足
|
解得-
| 37 |
| 14 |
| 17 |
| 10 |
点评:本题综合了数列,不等式以及函数的相关知识解题,难点在于构造函数f(n),利用函数性质解题;突破口是采取的思路是通性通法,顺着思路向下解题即可.

练习册系列答案
相关题目
若函数f(x)的导数为-2x2+1,则f(x)可以等于( )
| A、-2x3+1 | ||
B、-
| ||
| C、x+1 | ||
| D、-4x |
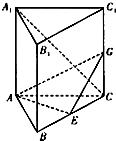 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.