题目内容
已知函数f(x)=
的值域为(-∞,1)∪(1,+∞),且f(2)=2.
(1)求f(x)的解析式;
(2)解不等式f(x)<
.
| nx |
| x+m |
(1)求f(x)的解析式;
(2)解不等式f(x)<
| 2x2 |
| x-1 |
考点:函数的值域
专题:函数的性质及应用
分析:(1)通过分离常数的方法将原函数变成f(x)=n-
,所以f(x)≠n,因为已知f(x)≠1,所以n=1,所以f(x)=
,在根据f(2)=2便可求出m=-1,所以f(x)的解析式便求得为f(x)=
;
(2)带入f(x)便可得到不等式:
<
,所以这时需讨论x-1>0,和x-1<0两种情况,这样不等式两边同乘以x-1即可将分式不等式变成整式不等式并求解即可.
| nm |
| x+m |
| x |
| x+m |
| x |
| x-1 |
(2)带入f(x)便可得到不等式:
| x |
| x-1 |
| 2x2 |
| x-1 |
解答:
解:(1)f(x)=
=n-
,∴f(x)≠n,由已知的f(x)值域知f(x)≠1;
∴n=1,f(x)=
,又f(2)=2,所以:
=2,∴m=-1;
∴f(x)=
;
(2)解
<
:
若x>1,由该不等式得x<2x2,解得x>
,或x<0,∴x>1;
若x<1,x>2x2,解得0<x<
,∴0<x<
;
∴原不等式的解为(0,
)∪(1,+∞).
| n(x+m)-nm |
| x+m |
| nm |
| x+m |
∴n=1,f(x)=
| x |
| x+m |
| 2 |
| 2+m |
∴f(x)=
| x |
| x-1 |
(2)解
| x |
| x-1 |
| 2x2 |
| x-1 |
若x>1,由该不等式得x<2x2,解得x>
| 1 |
| 2 |
若x<1,x>2x2,解得0<x<
| 1 |
| 2 |
| 1 |
| 2 |
∴原不等式的解为(0,
| 1 |
| 2 |
点评:考查函数值域的概念,以及分离常数法求值域,不等式两边同乘以一个式子需讨论式子的符号.

练习册系列答案
相关题目
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2
,则k的取值范围是( )
| 3 |
A、[-
| ||||||||
B、[-∞,-
| ||||||||
C、[-
| ||||||||
D、[-
|
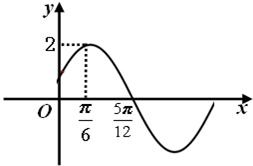 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<