题目内容
 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1,A1B1=A1C1,点D、F分别是棱BC、CC1上的中点,点E是CC1上的动点
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1,A1B1=A1C1,点D、F分别是棱BC、CC1上的中点,点E是CC1上的动点(Ⅰ)证明:A1F∥平面ADE;
(Ⅱ)证明:A1F⊥DE.
考点:直线与平面平行的判定,棱柱的结构特征,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)首先根据已知条件建立线线平行的条件,进一步利用线面平行的判定定理得到结论.
(Ⅱ)首先证明线面垂直,进一步转化成线线垂直.
(Ⅱ)首先证明线面垂直,进一步转化成线线垂直.
解答:
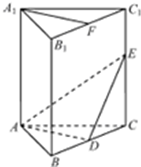 (Ⅰ) 证明:连结DF,在三棱柱ABC-A1B1C1中,BD,AC点D、F分别是棱BC、CC1上的中点,
(Ⅰ) 证明:连结DF,在三棱柱ABC-A1B1C1中,BD,AC点D、F分别是棱BC、CC1上的中点,
∴BD平行且等于B1F,
∴四边形BDFB1是平行四边形,
∴BB1平行且等于DF,
∴BB1平行且等于A
,
∴四边形AA1FD是平行四边形,
∴A1F∥AD,
又
?平面ADE,AD?平面ADE,
∴A1F∥平面ADE.
(Ⅱ)证明:由BB1⊥平面A1B1C1,又A1F?平面A1B1C1,
所以BB1⊥A1F,
在三角形A1B1C1中,A1B1=A1C1,且F为B1C1的中点,
所以B1C1⊥A1F,
又BB1∩B1C1=B1,
所以A1F⊥平面BCC1B1.
又点D、E分别是棱BC、CC1上的点,
所以DE?平面BCC1B1,所以A1F⊥DE.
 (Ⅰ) 证明:连结DF,在三棱柱ABC-A1B1C1中,BD,AC点D、F分别是棱BC、CC1上的中点,
(Ⅰ) 证明:连结DF,在三棱柱ABC-A1B1C1中,BD,AC点D、F分别是棱BC、CC1上的中点,∴BD平行且等于B1F,
∴四边形BDFB1是平行四边形,
∴BB1平行且等于DF,
∴BB1平行且等于A
| A | 1 |
∴四边形AA1FD是平行四边形,
∴A1F∥AD,
又
|
∴A1F∥平面ADE.
(Ⅱ)证明:由BB1⊥平面A1B1C1,又A1F?平面A1B1C1,
所以BB1⊥A1F,
在三角形A1B1C1中,A1B1=A1C1,且F为B1C1的中点,
所以B1C1⊥A1F,
又BB1∩B1C1=B1,
所以A1F⊥平面BCC1B1.
又点D、E分别是棱BC、CC1上的点,
所以DE?平面BCC1B1,所以A1F⊥DE.
点评:本题考查的知识要点:线面平行的判定定理,线面垂直的判定定理,线面垂直与线线垂直之间的转化,属于基础题型.

练习册系列答案
相关题目
有七名同学站成一排照毕业纪念照,其中小明必须站在正中间,并且小李、小张两位同学要站在一起,则不同的站法有( )
| A、192种 | B、120种 |
| C、96种 | D、48种 |
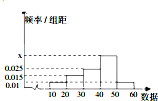 如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.
如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.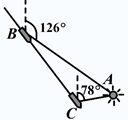 如图,货轮在海上以35nmile/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148°的方向航行.为了确定船位,在B点观察灯塔A的方位角是126°,航行半小时后到达C点,观察灯塔A的方位角是78°.求货轮到达C点时与灯塔A的距离(精确到0.01nmile).
如图,货轮在海上以35nmile/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148°的方向航行.为了确定船位,在B点观察灯塔A的方位角是126°,航行半小时后到达C点,观察灯塔A的方位角是78°.求货轮到达C点时与灯塔A的距离(精确到0.01nmile).