题目内容

抛物线3y2+2x=0的准线方程为
 
．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：把抛物线的方程化为标准方程，求出p值，确定开口方向，从而写出抛物线3y2+2x=0的准线方程．
解答： 解：抛物线的方程化为y2=-
2
3
x，焦点在x轴上，且开口向左，2p=
2
3

∴
p
2
=
1
6
．
∴抛物线3y2+2x=0的准线方程为x=
1
6
．
故答案为：x=
1
6
．
点评：本题考查抛物线的标准方程，考查抛物线的几何性质，定型与定位是关键．
练习册系列答案
相关题目
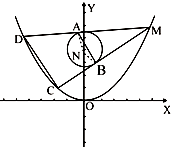设抛物线E：x2=2y，圆N：x2+（y-4）2=1
（1）若斜率为1，且过圆心N的直线l与抛物线E相交于P，Q两点，求|PQ|；
（2）点M是抛物线E上异于原点的一点，过点M作圆N的两条切线，切点分别为A，B，与抛物线E交于D，C两点，若四边形ABCD为梯形，求点M的坐标．
在△ABC中，角A，B，C所对的边分别为a，b，c，且cosA=
2
3
．
（Ⅰ）求2cos2
B+C
2
+sin2（B+C）；
（Ⅱ）若a=
3
，求△ABC面积的最大值．
已知函数f（x）=2sin2x-2sinxcos（x+
π
2
）．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）在区间[0，
π
2
]上的值域．
已知函数f（x）=2sin（
1
3
x+φ）（x∈R，0＜φ＜
π
2
）的图象过点M（
π
2
，
3
）．
（1）求φ的值；
（2）设α，β∈[0，
π
2
]，f（3α+π）=
10
13
，f（3β+
5π
2
）=-
6
5
，求sin（α-β）的值．
（
5x
-
1
x
）12的展开式中的常数项为
 
．
若直线x-y-1=0被⊙O：（x-a）2+y2=4所截得的弦长为2
2
，则实数a的值为
 
．
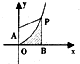如图，已知点A（0，1），点P（x0，y0）（x0＞0）在曲线y=x2上移动，过P点作PB⊥x轴于B，若曲线y=x2在第一象限内把梯形AOBP的面积平分，则P点的坐标为
 
．
执行如图所示的程序框图，则输出的S的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网