Question

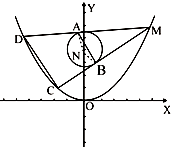设抛物线E：x²=2y，圆N：x²+（y-4）²=1
（1）若斜率为1，且过圆心N的直线l与抛物线E相交于P，Q两点，求|PQ|；
（2）点M是抛物线E上异于原点的一点，过点M作圆N的两条切线，切点分别为A，B，与抛物线E交于D，C两点，若四边形ABCD为梯形，求点M的坐标．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）斜率为1，且过圆心N的直线l的方程为y=x+4，代入抛物线方程，求出P，Q的横坐标，即可求|PQ|；
（2）求出过点M的圆N的切线方程，圆心N（0，4）到切线的距离，切线与抛物线联立，求出CD的斜率，若四边形ABCD是梯形，则由MN⊥AB知，MN⊥CD，所以k_MN•k_CD=-1，即可求点M的坐标．

解答： 解：（1）斜率为1，且过圆心N的直线l的方程为y=x+4，
由

x2=2y y=x+4

得 x²-2x-8=0，----------------（2分）
则x₁=-2，x₂=4，得|PQ|=

2

|x1-x2|=6

2

---------------------（4分）
（2）设M(x0，

x 2 0

2

)(x0≠0，x0≠±1)，过点M的圆N的切线方程为y-

x 2 0

2

=k(x-x0)，
即2kx-2y-2kx0+

x

2 0

=0，则圆心N（0，4）到切线的距离d=

| x 2 0 -2kx0-8|

4k2+4

=1，-------------（6分）
得(4-4

x

2 0

)k2+4x0(

x

2 0

-8)k+4-(

x

2 0

-8)2=0（*），
∴k_MC，k_MD是（*）的两根，kMC+kMD=

x0( x 2 0 -8)

x 2 0 -1

，
由

2kx-2y-2kx0+ x 2 0 =0 x2=2y

得x2-2kx+2kx0-

x

2 0

=0，
∴

xD+x0=2kMD xC+x0=2kMC

，
∴x_C+x_D=2（k_MC+k_MD）-2x₀，
∴kCD=

x 2 C 2 - x 2 D 2

xC-xD

=

xC+xD

2

=(kMC+kMD)-x0=

7x0

1- x 2 0

，------------（10分）
若四边形ABCD是梯形，则由MN⊥AB知，MN⊥CD，所以k_MN•k_CD=-1，--------------（12分）
∴

7x0

1- x 2 0

•

x 2 0 2 -4

x0

=-1⇒

x

2 0

=

54

5

⇒x0=±

3 30

5

，
故M（

3

5

30

，

27

5

）或M（-

3

5

30

，

27

5

）-------------（14分）

点评：本题考查直线与抛物线的位置关系，考查弦长的计算，考查韦达定理的运用，考查学生分析解决问题的能力，属于中档题．