题目内容
若直线x-y-1=0被⊙O:(x-a)2+y2=4所截得的弦长为2
,则实数a的值为 .
| 2 |
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意利用弦长公式求得圆心(a,0)到直线距离d=
,再由圆心到直线距离公式可得
=
,由此求得a的值.
| 2 |
| |a-0-1| | ||
|
| 2 |
解答:
解:由题意可得圆的半径r=2,半弦长
,从而圆心(a,0)到直线距离d=
.
由圆心到直线距离公式可得
=
,求得a=-1,或a=3,
故答案为:-1或3.
| 2 |
| 2 |
由圆心到直线距离公式可得
| |a-0-1| | ||
|
| 2 |
故答案为:-1或3.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
如果复数(m-i)i(其中m∈R)的实部与虚部互为相反数,则m=( )
| A、2 | B、-2 | C、-1 | D、1 |
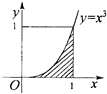 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为