题目内容
将A,B,C,D,E五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件A,B被放在相邻的抽屉内且文件C,D被放在不相邻的抽屉内的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等可能事件的概率
专题:计算题,概率与统计
分析:先用捆绑法,将A,B看成一个元素,相应的抽屉看成6个,把4个元素在6个位置排列,由排列数公式可得其排列数目;再求A,B和C,D也相邻的排列数目,用间接法求得A,B被放在相邻的抽屉内且文件C,D被放在不相邻的抽屉内的排列数目;根据将A,B,C,D,E五种不同的文件随机地放入七个抽屉内,每个抽屈至多放一种文件,共
种方法,代入古典概型概率公式计算.
| A | 5 7 |
解答:
解:将A,B,C,D,E五种不同的文件随机地放入七个抽屉内,每个抽屈至多放一种文件,共有
种方法;
文件A,B被放在相邻的抽屉内,
∴A,B看成一个元素,相应的抽屉看成6个,则有4个元素在6个位置排列,
∴有
=720种方法;
文件A,B被放在相邻的抽屉内且文件C,D被放在相邻的抽屉内,有A22A22A53=240种方法,
∴文件A,B被放在相邻的抽屉内且文件C,D被放在不相邻的抽屉内,有720-240=480种方法.
∴文件A,B被放在相邻的抽屉内且文件C,D被放在不相邻的抽屉内的概率为
=
.
故选:B.
| A | 5 7 |
文件A,B被放在相邻的抽屉内,
∴A,B看成一个元素,相应的抽屉看成6个,则有4个元素在6个位置排列,
∴有
| A | 2 2 |
| A | 4 6 |
文件A,B被放在相邻的抽屉内且文件C,D被放在相邻的抽屉内,有A22A22A53=240种方法,
∴文件A,B被放在相邻的抽屉内且文件C,D被放在不相邻的抽屉内,有720-240=480种方法.
∴文件A,B被放在相邻的抽屉内且文件C,D被放在不相邻的抽屉内的概率为
| 480 |
| 7×6×5×4×3 |
| 4 |
| 21 |
故选:B.
点评:本题考查了排列、组合的运用,本题采用了解排列组合的常用方法间接法与捆绑法,两个元素相邻的问题,一般把这两个元素看成一个元素进行排列,注意这两个元素内部还有一个排列.

练习册系列答案
相关题目
一个各项均为正数的等比数列,其任何一项都等于它后面两项之和,则其公比是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知集合M={x|
>0},N={x|-3x2+x+2>0},则M∩N=( )
| 2x-1 |
| x+1 |
| A、(-∞,-1)∪(1,+∞) | ||
B、(
| ||
| C、(1,+∞) | ||
D、(-∞,-1)∪(-
|
现有5名同学去听同时进行的6个课外知识讲座,每名同学可自由选择其中的一个讲座,不同选法的种数是( )
| A、54 | ||
| B、65 | ||
C、
| ||
| D、6×5×4×3×2 |
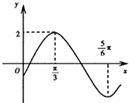
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则( )
| π |
| 2 |

A、ω=1,φ=
| ||
B、ω=1,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.