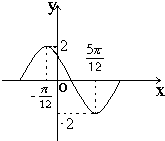
题目内容
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则( )
| π |
| 2 |

A、ω=1,φ=
| ||
B、ω=1,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
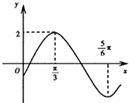
分析:根据图象求出A和周期T,再由周期公式求出ω的值,再把图象上的点坐标(
,0)代入解析式,根据条件和特殊角的正弦值求出φ的值.
| π |
| 3 |
解答:
解:由图得,A=2,
T=
-
,则T=π,
∴
=π,解得ω=2,
又图象过点(
,2),
∴2sin(2×
+φ)=2,则sin(
+φ)=1,
∵|φ|<
,∴
+φ=
,
解得φ=-
,
故选:D.
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 3 |
∴
| 2π |
| ω |
又图象过点(
| π |
| 3 |
∴2sin(2×
| π |
| 3 |
| 2π |
| 3 |
∵|φ|<
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
解得φ=-
| π |
| 6 |
故选:D.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得φ是关键,也是难点,考查识图能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
设全集为U,集合A与集合B的关系如图,则下列说法正确的是( )


| A、对任意a∈A,都有a∉B |
| B、不存在b∈B,使b∈A |
| C、对任意c∈∁UA都有c∈B |
| D、存在d∈B,使d∈∁UA |
乒乓球运动员10人,其中男女运动员各5人,从这10名运动员中选出4人进行男女混合双打比赛,选法种数为( )
A、(A
| ||||
B、(C
| ||||
C、(C
| ||||
D、(C
|
用”辗转相除法”求得98与63的最大公约数是( )
| A、17 | B、14 | C、9 | D、7 |
已知向量
=(0,1),
=(1,0),
=(3,4),若λ为实数,且(
+λ
)⊥
,则λ的值为( )
| a |
| b |
| c |
| b |
| a |
| c |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
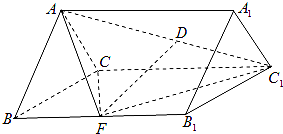 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.