题目内容
已知Sn是等差数列{an}的前n项和,满足a3=4,S7=35;Tn是数列{bn}的前n项和,满足:Tn=2bn-2(n∈N*).
(1)求数列{an},{bn}的通项公式;
(2)求数列{
}的前n项和Rn.
(1)求数列{an},{bn}的通项公式;
(2)求数列{
| 1 |
| an•(log2bn) |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式和前n项和公式列出方程组,求出数列的首项和公差,由此能求出数列{an}的通项公式;由已知条件推导出{bn}是以2为公比的等比数列,由此能求出数列{bn}的通项公式.
(2)由
=
=
=
-
,利用裂项求和法能求出
数列{
}的前n项和Rn.
(2)由
| 1 |
| an•(log2bn) |
| 1 |
| (n+1)•(log22n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
数列{
| 1 |
| an•(log2bn) |
解答:
(本题共12分)
(1)解:设等差数列{an}的公差d,
∵a3=4,S7=35,∴
,
解得a1=2,d=1,
∴an=2+(n-1)×1=n+1.…(3分)
Tn=2bn-2,Tn-1=2bn-1-2,(n≥2,n∈N*)
两式相减得:bn=2bn-2bn-1,
∴bn=2bn-1,且n=1也满足,
∴{bn}是以2为公比的等比数列,
又∵b1=2,∴bn=2n.…(7分)
(2)解:∵
=
=
=
-
,
∴Rn=1-
+
-
+…+
-
=1-
=
.…(12分)
(1)解:设等差数列{an}的公差d,
∵a3=4,S7=35,∴
|
解得a1=2,d=1,
∴an=2+(n-1)×1=n+1.…(3分)
Tn=2bn-2,Tn-1=2bn-1-2,(n≥2,n∈N*)
两式相减得:bn=2bn-2bn-1,
∴bn=2bn-1,且n=1也满足,
∴{bn}是以2为公比的等比数列,
又∵b1=2,∴bn=2n.…(7分)
(2)解:∵
| 1 |
| an•(log2bn) |
| 1 |
| (n+1)•(log22n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Rn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离.
如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离. 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.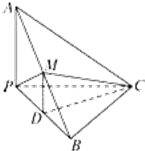 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.