题目内容
解不等式mx2+(m-1)x-1≥0.
考点:一元二次不等式的解法
专题:分类讨论,不等式的解法及应用
分析:讨论m=0、m>0和m<0时,不等式的解集是什么,解答即可.
解答:
解:m=0时,原不等式可化为-x-1≥0,解得x≤-1;
m>0时,原不等式可化为(x-
)(x+1)≥0,又
>-1,
∴解得x≤-1,x≥
;
m<0时,原不等式可化为(x-
)(x+1)≤0,
当
<-1,即-1<m<0时,解得
≤x≤-1;
当
=-1,即m=-1时,解得x=-1;
当0>
>-1,即m<-1时,解得-1≤x≤
;
综上,m=0时,原不等式的解集是(-∞,-1];
m>0时,原不等式的解集是(-∞,-1]∪[
,+∞);
-1<m<0时,原不等式的解集为[
,-1];
m=-1时,原不等式的解集为{x|x=-1};
m<-1时,原不等式的解集为[-1,
].
m>0时,原不等式可化为(x-
| 1 |
| m |
| 1 |
| m |
∴解得x≤-1,x≥
| 1 |
| m |
m<0时,原不等式可化为(x-
| 1 |
| m |
当
| 1 |
| m |
| 1 |
| m |
当
| 1 |
| m |
当0>
| 1 |
| m |
| 1 |
| m |
综上,m=0时,原不等式的解集是(-∞,-1];
m>0时,原不等式的解集是(-∞,-1]∪[
| 1 |
| m |
-1<m<0时,原不等式的解集为[
| 1 |
| m |
m=-1时,原不等式的解集为{x|x=-1};
m<-1时,原不等式的解集为[-1,
| 1 |
| m |
点评:本题考查了含有字母系数的不等式的解法问题,解题时应对字母系数进行讨论,是易错题.

练习册系列答案
相关题目
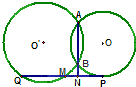 如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.
如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.