题目内容
设f(x)是二次函数,方程f(x)=0有两个相等实根,且f′(x)=2x+2
(Ⅰ)求y=f(x)的表达式
(Ⅱ)求y=f(x)与函数y=-x2+5围成的图形面积.
(Ⅰ)求y=f(x)的表达式
(Ⅱ)求y=f(x)与函数y=-x2+5围成的图形面积.
考点:导数的运算,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)根据导函数的解析式设出原函数的解析式,根据有两个相等的实根可得答案.
(2)先由解方程组求出积分区间,再通过求定积分求出即可.
(2)先由解方程组求出积分区间,再通过求定积分求出即可.
解答:
解:(1)∵f′(x)=2x+2 设f(x)=x2+2x+c,
根据f(x)=0有两等根,得△=4-4c=0解得c=1,即f(x)=x2+2x+1;
(2)由
解得x=-2,或x=1,
∴y=f(x)与函数y=-x2+5围成的图形面积S=
[-x2+5-(x2+2x+1)]dx=(-
x3-x2+4x)
=9.
根据f(x)=0有两等根,得△=4-4c=0解得c=1,即f(x)=x2+2x+1;
(2)由
|
∴y=f(x)与函数y=-x2+5围成的图形面积S=
| ∫ | 1 -2 |
| 2 |
| 3 |
| | | 1 -2 |
点评:本题主要考查导数的逆运算和定积分在求面积中的应用.属基础题.

练习册系列答案
相关题目
若函数f(x)=x3-ax2+4在(0,2)内单调递减,则实数a的取值范围为( )
| A、[3,+∞) |
| B、{3} |
| C、(-∞,3] |
| D、(0,3) |
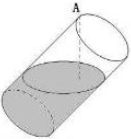 一空的圆柱体容器直径小于母线长斜放,将容器斜放,使圆柱的母线与水平面成45°角,现于这种状态下由容器的最高点A处匀速地灌油,如图,则点A到油平面的距离y与灌水时间t的函数图象大致为( )
一空的圆柱体容器直径小于母线长斜放,将容器斜放,使圆柱的母线与水平面成45°角,现于这种状态下由容器的最高点A处匀速地灌油,如图,则点A到油平面的距离y与灌水时间t的函数图象大致为( )A、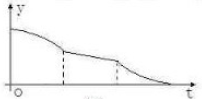 |
B、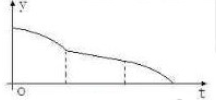 |
C、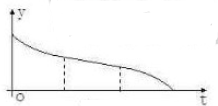 |
D、 |
已知集合A={x|-1<x<1},则下列选项中正确的是( )
| A、0⊆A | B、{0}∈A |
| C、∅∈A | D、{0}⊆A |