题目内容
(1+x)2n(n∈N*)的展开式中,系数最大的项是第 项.
考点:二项式系数的性质
专题:二项式定理
分析:本题中第r+1项的系数与第r+1项的二项式系数相同,再根据中间项的二项式系数最大,展开式共有2n+1项,可得第n+1项的系数最大.
解答:
解:在(1+x)2n(n∈N*)的展开式中,第r+1项的系数与第r+1项的二项式系数相同,
再根据中间项的二项式系数最大,展开式共有2n+1项,可得第n+1项的系数最大,
故答案为:n+1.
再根据中间项的二项式系数最大,展开式共有2n+1项,可得第n+1项的系数最大,
故答案为:n+1.
点评:本题主要考查二项式定理的应用,二项式系数的性质,注意各项系数和与各项的二项式系数和的区别,属于基础题.

练习册系列答案
相关题目
设数列{an}是等比数列,满足an>0,q>1,且a3+a5=20,a2•a6=64,则a6=( )
| A、16 | B、32 | C、42 | D、48 |
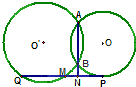 如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.
如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.