题目内容
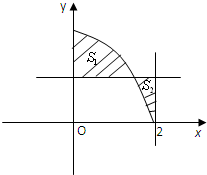如图，已知S1为直线x=0，y=4-t2及y=4-x2所围成的面积，S2为直线x=2，y=4-t2及y=4-x2所围成图形的面积（t为常数）．（1）若t=
| 2 |
（2）若t∈（0，2），求S1+S2的最小值．
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：（1）利用定积分表示出S2；
（2）若t∈（0，2），利用定积分表示出S1+S2，利用函数的单调性求最小值．
（2）若t∈（0，2），利用定积分表示出S1+S2，利用函数的单调性求最小值．
解答：
解：（1）当t=
时，S2=
[2-（4-x2）]dx=（
x3-2x）
=
（
-1）．…（5分）
（2）t∈（0，2），S1=
[（4-x2）-（4-t2）]dx=（t2x-
x3）
=
t3，…（6分）
S2=
[（4-t2）-（4-x2）]dx=（
x3-t2x）
=
-2t2+
t3，…（7分）
∴S=S1+S2=
t3-2t2+
，…（8分）
∴S′=4t（t-1），
令S′=0得t=0（舍去）或t=1，
当0＜t＜1时，S′＜0，S单调递减，
当t＞1时，S′＞0，S单调递增，
∴当t=1时，Smin=2．…（13分）
| 2 |
| ∫ | 2
|
| 1 |
| 3 |
| | | 2
|
| 4 |
| 3 |
| 2 |
（2）t∈（0，2），S1=
| ∫ | t 0 |
| 1 |
| 3 |
| | | t 0 |
| 2 |
| 3 |
S2=
| ∫ | 2 t |
| 1 |
| 3 |
| | | t 0 |
| 8 |
| 3 |
| 2 |
| 3 |
∴S=S1+S2=
| 4 |
| 3 |
| 8 |
| 3 |
∴S′=4t（t-1），
令S′=0得t=0（舍去）或t=1，
当0＜t＜1时，S′＜0，S单调递减，
当t＞1时，S′＞0，S单调递增，
∴当t=1时，Smin=2．…（13分）
点评：本题考查定积分在求面积中的应用，考查导数知识的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知集合A={x|-1＜x＜1}，则下列选项中正确的是（ ）
| A、0⊆A | B、{0}∈A |
| C、∅∈A | D、{0}⊆A |
已知圆O：x2+y2=4，直线l：kx-y-k-1=0