题目内容
已知-
＜x＜
，sinx+cosx=
，求tanx的值．
| π |
| 2 |
| π |
| 2 |
| 1 |
| 5 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：将已知等式两边平方求出2sinxcosx的值，再利用完全平方公式列出关系式，将2sinxcosx的值代入，开方求出sinx-cosx的值，联立求出sinx与cosx的值，即可确定出tanx的值．
解答：
解：由sinx+cosx=
，得：（sinx+cosx）2=sin2x+2sinxcosx+cos2x=1+2sinxcosx=
，
整理得：2sinxcosx=-
，
∴（sinx-cosx）2=sin2x-2sinxcosx+cos2x=1-2sinxcosx=
，
∵sinxcosx＜0，
∴-
＜x＜0，
∴cosx-sinx=
，
又∵sinx+cosx=
，
∴cosx=
，sinx=-
．
∴tanx=-
．
| 1 |
| 5 |
| 1 |
| 25 |
整理得：2sinxcosx=-
| 24 |
| 25 |
∴（sinx-cosx）2=sin2x-2sinxcosx+cos2x=1-2sinxcosx=
| 49 |
| 25 |
∵sinxcosx＜0，
∴-
| π |
| 2 |
∴cosx-sinx=
| 7 |
| 5 |
又∵sinx+cosx=
| 1 |
| 5 |
∴cosx=
| 4 |
| 5 |
| 3 |
| 5 |
∴tanx=-
| 3 |
| 4 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
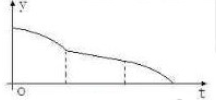
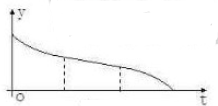
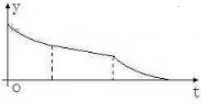
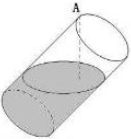一空的圆柱体容器直径小于母线长斜放，将容器斜放，使圆柱的母线与水平面成45°角，现于这种状态下由容器的最高点A处匀速地灌油，如图，则点A到油平面的距离y与灌水时间t的函数图象大致为（ ）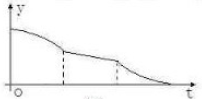
已知圆O：x2+y2=4，直线l：kx-y-k-1=0