题目内容
已知函数f（x）=
，且关于x的方程f（x）+x-a=0有且只有一个实根，则实数a的取值范围是 ．
|
考点：分段函数的应用
专题：计算题,数形结合,函数的性质及应用
分析：关于x的方程f（x）+x-a=0有且只有一个实根?y=f（x）与y=-x+a的图象只有一个交点，结合图象即可求得．
解答：
解：关于x的方程f（x）+x-a=0有且只有一个实根?y=f（x）
与y=-x+a的图象只有一个交点，画出函数的图象如右图，
观察函数的图象可知当a＞1时，y=f（x）与y=-x+a的图象
只有一个交点，即有a＞1．
故答案为：（1，+∞）
解：关于x的方程f（x）+x-a=0有且只有一个实根?y=f（x）与y=-x+a的图象只有一个交点，画出函数的图象如右图，
观察函数的图象可知当a＞1时，y=f（x）与y=-x+a的图象
只有一个交点，即有a＞1．
故答案为：（1，+∞）
点评：本题主要考查了指数函数、对数函数的图象性质；但要注意函数的图象的分界点，考查利用图象综合解决方程根的个数问题．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
已知a是实数，
是纯虚数，则a等于（ ）
| a+i |
| 1-i |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
下列函数中，既是偶函数又在区间（-∞，0）上单调递减的是（ ）
| A、y=lg|x| | ||
B、y=
| ||
| C、y=-x2+1 | ||
| D、y=e-x |
函数f（x）=|x+1|在[-2，2]上的最小值为（ ）
| A、5 | B、2 | C、1 | D、0 |
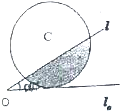如图，已知直线l和圆C，当l从l0开始在平面上绕点O按逆时针方向匀速转动（转动角度不超过90°）时，它扫过的圆内阴影部分的面积y是时间x的函数，这个函数的图象大致是（ ）
