题目内容
19．执行如图的程序框图，若结束时输出的结果不小于3，则t的取值范围为（ ）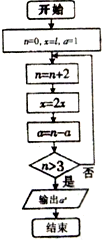
| A． | t≥$\frac{1}{4}$ | B． | t≥$\frac{1}{8}$ | C． | t≤$\frac{1}{4}$ | D． | t≤$\frac{1}{8}$ |
分析 第一次执行循环结构：n←0+2，第二次执行循环结构：n←2+2，此时应终止循环结构．求出相应的x、a即可得出结果．
解答 解：第一次执行循环结构：n←0+2，x←2×t，a←2-1；
∵n=2＜3，
∴继续执行循环结构；
第二次执行循环结构：n←2+2，x←2×2t，a←4-1；
∵n=4＞3，
∴应终止循环结构，并输出34t．
由于结束时输出的结果不小于3，
故34t≥3，即4t≥1，解得t$≥\frac{1}{4}$．
故选：A．
点评 理解循环结构的功能和判断框的条件是解决问题的关键，属基础题．
练习册系列答案
相关题目
10．已知△ABC中，三个内角A，B，C的对边分别为a，b，c，若asinA-csinC=（a-b）sinB．角C=（ ）
| A． | 30° | B． | 60° | C． | 120° | D． | 150° |
4．设集合A={0，1}，集合B={x|x＞a}，若A∩B=∅，则实数a的范围是（ ）
| A． | a≤1 | B． | a≥1 | C． | a≥0 | D． | a≤0 |
11．
2014年12月28日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）
已知在北京地铁四号线上，任意一站到陶然亭站的票价不超过5元，现从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选出120人，他们乘坐地铁的票价统计如图所示．
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1人，试估计此人乘坐地铁的票价小于5元的概率；
（Ⅱ）已知选出的120人中有6名学生，且这6人乘坐地铁的票价情形恰好与按票价从这120人中分层抽样所选的结果相同，现从这6人中随机选出2人，求这2人的票价和恰好为8元的概率；
（Ⅲ）小李乘坐地铁从A地到陶然亭的票价是5元，返程时，小李乘坐某路公共电汽车所花交通费也是5元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s公里，试写出s的取值范围．（只需写出结论）
2014年12月28日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）| 乘公共电汽车方案 | 10公里（含）内2元； 10公里以上部分，每增加1元可乘坐5公里（含）． |
乘坐地铁方案（不含机场线） | 6公里（含）内3元； 6公里至12公里（含）4元； 12公里至22公里（含）5元； 22公里至32公里（含）6元； 32公里以上部分，每增加1元可乘坐20公里（含）． |
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1人，试估计此人乘坐地铁的票价小于5元的概率；
（Ⅱ）已知选出的120人中有6名学生，且这6人乘坐地铁的票价情形恰好与按票价从这120人中分层抽样所选的结果相同，现从这6人中随机选出2人，求这2人的票价和恰好为8元的概率；
（Ⅲ）小李乘坐地铁从A地到陶然亭的票价是5元，返程时，小李乘坐某路公共电汽车所花交通费也是5元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s公里，试写出s的取值范围．（只需写出结论）
在角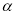
的终边上，则
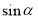的值为（ ）
B．
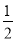D．