题目内容
4.设集合A={0,1},集合B={x|x>a},若A∩B=∅,则实数a的范围是( )| A. | a≤1 | B. | a≥1 | C. | a≥0 | D. | a≤0 |
分析 由A∩B=∅,可知集合B中最小元素要大于等于集合A中最大元素,即得答案.
解答 解:∵集合A={0,1},集合B={x|x>a},且A∩B=∅,
∴集合B中最小元素要大于等于集合A中最大元素,
从而a≥1,
故选:B.
点评 本题考查集合的运算,弄清交集的定义是解决本题的关键,属基础题.

练习册系列答案
相关题目
19.执行如图的程序框图,若结束时输出的结果不小于3,则t的取值范围为( )
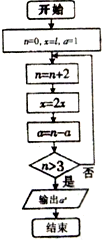

| A. | t≥$\frac{1}{4}$ | B. | t≥$\frac{1}{8}$ | C. | t≤$\frac{1}{4}$ | D. | t≤$\frac{1}{8}$ |
9.某赛事组委会要为获奖者定做某工艺品作为奖品,其中一等奖奖品3件,二等奖奖品6件.制作一等奖和二等奖奖品所用原料完全相同,但工艺不同,故价格有所差异.现有甲、乙两家工厂可以制作奖品(一等奖、二等奖奖品均符合要求),甲厂收费便宜,但原料有限,最多只能制作4件奖品,乙厂原料充足,但收费较贵,其具体收费情况如下表:
则组委会定做该工艺品的费用总和最低为4900元.
奖品 收费(元/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
 某学校拟建一块周长为400米的操场,如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,矩形的长应该设计成100米.
某学校拟建一块周长为400米的操场,如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,矩形的长应该设计成100米. 的离心率为
的离心率为 ,以
,以 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. 的标准方程;
的标准方程; ,和面内一点
,和面内一点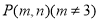 ,过点
,过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若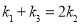 ,试求
,试求 满足的关系式.
满足的关系式.