题目内容
10．已知△ABC中，三个内角A，B，C的对边分别为a，b，c，若asinA-csinC=（a-b）sinB．角C=（ ）| A． | 30° | B． | 60° | C． | 120° | D． | 150° |
分析 由正弦定理可得，sinA=$\frac{a}{2R}$，sinB=$\frac{b}{2R}$，sinC=$\frac{c}{2R}$，代入条件可得三边的关系，再由余弦定理，结合特殊角的三角函数值，即可求得角C．
解答 解：由正弦定理可得，sinA=$\frac{a}{2R}$，sinB=$\frac{b}{2R}$，sinC=$\frac{c}{2R}$，
asinA-csinC=（a-b）sinB即为
a2-c2=（a-b）b，
即有a2+b2-c2=ab，
由余弦定理，可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{ab}{2ab}$=$\frac{1}{2}$，
由于C为三角形的内角，
则C=60°．
故选：B．
点评 本题考查正弦定理和余弦定理的运用，同时考查特殊角的三角函数值，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
1．某商场每天（开始营业时）以每件150元的价格购入A商品若干件（A商品在商场的保鲜时间为10小时，该商场的营业时间也恰好为10小时），并开始以每件300元的价格出售，若前6小时内所购进的商品没有售完，则商店对没卖出的A商品以每件100元的价格低价处理完毕（根据经验，4小时内完全能够把A商品低价处理完毕，且处理完后，当天不再购进A商品）．该商场统计了100天A商品在每天的前6小时内的销售量，制成如下表格（注：视频率为概率）．（其中x+y=70）
（Ⅰ）若某该商场共购入6件该商品，在前6个小时中售出4件．若这些产品被6名不同的顾客购买，现从这6名顾客中随机选2人进行回访，则恰好一个是以300元价格购买的顾客，另一个以100元价格购买的顾客的概率是多少？
（Ⅱ）若商场每天在购进5件A商品时所获得的平均利润最大，求x的取值范围．
| 前6小时内的销售量t（单位：件） | 4 | 5 | 6 |
| 频数 | 30 | x | y |
（Ⅱ）若商场每天在购进5件A商品时所获得的平均利润最大，求x的取值范围．
19．执行如图的程序框图，若结束时输出的结果不小于3，则t的取值范围为（ ）
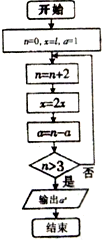
| A． | t≥$\frac{1}{4}$ | B． | t≥$\frac{1}{8}$ | C． | t≤$\frac{1}{4}$ | D． | t≤$\frac{1}{8}$ |
20．
如图是用计算机随机模拟的方法估计概率的程序框图，P表示估计结果，则输出P的近似值为（ ）
如图是用计算机随机模拟的方法估计概率的程序框图，P表示估计结果，则输出P的近似值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{8}$ |